Introduction to Trigonometry Class 10 MCQ with Answers – Maths Class 10 MCQ Online Test are covered in this Article. Introduction to Trigonometry Class 10 MCQ Test contains 30 questions. Answers to MCQ on Introduction to Trigonometry Class 10 are available after clicking on the answer. MCQ Questions for Class 10 with Answers have been made for Class 10 students to help check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Board | CBSE |
| Textbook | Maths (NCERT) |
| Class | Class 10 |
| Chapter | Chapter 8 Introduction to Trigonometry |
| Category | MCQ Questions for Class 10 Maths with Answers |
Introduction to Trigonometry Class 10 MCQ with Answers
1. The trigonometric ratios of an acute angle in a right triangle express the relationship between
(a) the angle and the length of its sides
(b) only sides
(c) only angles
(d) None of these
Answer
Answer: (a) the angle and the length of its sides
Explanation: The trigonometric ratios of an acute angle in a right triangle express the relationship between
the angle and the length of its sides
2.
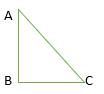
In Δ ABC, trigonometric ratio of Sine ∠C is
(a)AB/AC
(b)AC/AB
(c) AB/BC
(d)BC/AC
Answer
Answer: (a)AB/AC
Explanation: Sine∠c = (side opposite to ∠c )/Hypotenuse = AB/AC
3. Value of Sin 30 is
(a)1
(b)0
(c)1/2
(d)1/3
Answer
Answer: (c) 1/2
Explanation: sin30=1/2
4. Value of Sin30 Cos60 is
(a)1/4
(b)1/3
(c)2/3
(d)1/2
Answer
Answer: (a)1/4
Explanation: We know,
sin 30= 1/2
and cos 60 = 1/2
sin30 cos60 = 1/2×1/2
=1/4
5. 3sec30 Cos60 is
(a)1
(b)√1
(c)√2
(d)√3
Answer
Answer: (d)√3
Explanation:
sec30 = 2/(√3),
cos60 =1/2
3 sec30 cos60 = 3×2/(√3) ×1/2
= √3
6. 3 Sin45 Sec60 + 3Cos30 tan45 =
(a)3[√2+√3]
(b)(3/2) [2√2 +√3]
(c)[2√2 +√3]
(d) (3/2) [√2 +√3]
Answer
Answer: (b)(3/2) [2√2 +√3]
Explanation:
sin45 = 1/(√2),
sec60= 2,
cos30=(√3)/2,
tan45=1
3 sin45 sec60 + 3cos30 tan45 = 3×1/(√2)×2 + 3×(√3)/2×1
= 3 [ √2+(√3)/2]
= 3/2 [ 2√2+√3]
7. If tan 3x = cot230/√3 ,then value of x is
(a)45
(b)35
(c) 20
(d)30
Answer
Answer: (c) 20
Explanation:
cot 30 = √3 ,
cot2 30=(√3)2 = 3
tan 3x = (cot2 30)/√3
tan 3x = 3/√3
tan 3x = √3
tan 3x =tan 60
3x = 60
X = 20
Introduction to Trigonometry Class 10 MCQ with Answers
8. If cosec x =2 then value of x is
(a)10
(b) 15
(c)20
(d)30
Answer
Answer: (d)30
Explanation: cosec 30 = 2
Cosec x = 2
Cosec x = cosec 30
x = 30
9. If x =30, then value of 4cos2x -1 /(2sin2x) is
(a) 1/√3
(b) 1
(c) 3/√2
(d) 0
Answer
Answer: (a) 1/√3
Explanation:
cos 60 = 1/2 ,
sin 60 = (√3)/2
(cos2x-1)/(2 sin2x)=(4cos2×30-1)/(2 sin2×30)
= (4cos60-1)/(2 sin60)
=(4×1/2-1)/(2×(√3)/2)
=(2-1)/(√3)
=1/(√3)
10. sin2 60 is
(a) √3/2
(b) 3/2
(c) 3/4
(d) 3/6
Answer
Answer: (c) 3/4
Explanation:
sin 60 = (√3)/2
sin260 = ((√3)/2)2
= 3/4
11. In Δ ABC , right angled at B, AB=3 cm and BC = 4 cm. The value of tan c is
(a) 3/5
(b) 9/16
(c) 4/3
(d) 3/4
Answer
Answer: (d) 3/4
Explanation:
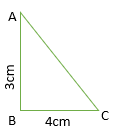
tan c = (opposite side)/(adjacent side)
= 3/4
12. (cos60 + sin30) /(1+cos30 + sin60) =
(a) 1/(1+√3)
(b) √3/2
(c) 1/(2+√3)
(d) 1/(2+2√3)
Answer
Answer: (a) 1/(1+√3)
Explanation:
cos 60 = 1/2 ,
cos 30 = (√3)/2 ,
sin 60 = (√3)/2 ,
sin 30 = 1/2
cos60 + sin30 /(1+cos30 + sin60)
= (1/2+1/2)/(1+(√3)/2+(√3)/2)
= 1/((2+√3+√3)/2)
= 1/((2+2√3)/2)
=1/(1+√3)
13. 2 sin260 + cos60=
(a) 0
(b) 1
(c) 2
(d) 3
Answer
Answer: (c) 2
Explanation:
sin 60 = (√3)/2 ,
cos 60 = 1/2
2 sin260 + cos60
= 2 (√3/2)2 + 1/2
= 2 (3/4) +1/2
= 3/2 +1/2
= 4/2 = 2
14. (2tan30)/(1+ tan230) =
(a)sin30
(b) sin60
(c) cos45
(d) Cos60
Answer
Answer: (b) sin60
Explanation:
tan 30 = 1/√3 ,
tan2 30=(1/√3)= 1/3
(2 tan30)/(1+tan2 30)
= (2 (1/√3))/(1+1/3)
= (2 (1/√3))/(4/3)
= (2/√3)/(4/3)
= 2/√3×3/4
= (√3)/2
= sin 60
15. (1/3) tan260 – 4 sin2 30 – (1/2) cosec245 + sec260 =
(a)3
(b)2
(c) 1
(d) None of these
Answer
Answer: (a)3
Explanation:
sin 30 = 1/2 ,
tan 60 = √3 ,
cosec 45 = √2 ,
sec 60 =2
(1/3) tan260 – 4 sin2 30 – (1/2) cosec245 + sec260 =
= (1/3)(√3 )2– (4) (1/2)2– (1/2) (√2 )2+(2)2
= (1/3)(3)– (4) (1/4)- (1/2) (2)+4
= 1-1-1+4 = 3
16. sin2 θ + cos2 θ=
(a)1
(b)0
(c) 2
(d) None of these
Answer
Answer: (a)1
17. 1 – sin2 θ =
(a) sin2 θ
(b) cos2 θ
(c) sin2 θ + cos2 θ
(d)0
Answer
Answer: (b) cos2 θ
Explanation:
We know,
sin2 θ + cos2 θ =1
1-sin2 θ = cos2 θ
Introduction to Trigonometry Class 10 MCQ with Answers
18. sin4 θ – cos4 θ=
(a) 1+2sin2 θ
(b) 1-sin2 θ
(c) 2sin2 θ-1
(d) sin2 θ + 1
Answer
Answer: (c) 2sin2 θ-1
Explanation: sin4 θ – cos4 θ=
(sin2 θ)2 -(cos2 θ)2
= (sin2 θ + cos2 θ) (sin2 θ – cos2 θ)
= 1 (sin2 θ – cos2 θ)
= (sin2 θ -(1-sin2 θ)
= (2sin2 θ-1)
19. √(1-cosA)/(1+cosA) =
(a) cosec A – cot A
(b) cosec A + cot A
(c) cot A -cosec A
(d) cosec A
Answer
Answer: (a) cosec A – cot A
Explanation: √(1-cosA)/(1+cosA )
=√(1-cosA)/(1+cosA ) ×(1-cosA)/(1-cosA )
= √(1-cosA)2/(1-cos2A)
= √(1-cosA)2/(sin2 A)
= (1-cosA)/sinA
= 1/sinA -cosA/sinA
= cosec A – cot A
20. sin8 θ – cos8 θ -(2sin2 θ – 1)=
(a) (2sin2 θ – 1)
(b) (2sin2 θ +1)
(c) 0
(d)None of these
Answer
Answer: (d)None of these
Explanation: sin8 θ – cos8 θ – (2sin2 θ – 1)
= (sin4 θ)2 – (cos4 θ)2 -(2sin2 θ – 1)
= (sin4 θ + cos4 θ) (sin4 θ -cos4 θ ) -(2sin2 θ – 1)
= { (sin2 θ)2 + (cos2 θ)2 } { (sin2 θ)^2 – (cos2 θ)^2 } – (2sin2 θ – 1)
= { (sin2 θ + cos2 θ)2 – 2sin2 θ cos2 θ} { (sin2 θ + cos2 θ) (sin2 θ – cos2 θ) } – (2sin2 θ – 1)
= { 1 – 2sin2 θ cos2 θ} { (sin2 θ – cos2 θ) } – (2sin2 θ – 1)
= { 1 – 2sin2 θ cos2 θ} {sin2 θ -(1- sin2)
21. Sec A =
(a)sin A
(b) 1/sin A
(c) cos A
(d)1/cos A
Answer
Answer: (d)1/cos A
22. If sin θ – cos θ = p and sec θ – cosec θ = q , then q(p2-1) =
(a)p
(b) -2p
(c)2p
(d) None of these
Answer
Answer: (b) -2p
Explanation: Given sinθ-cosθ=p and secθ -cosecθ=q
q(p2-1) = (secθ -cosecθ)[(sinθ -cosθ)2-1]
= (secθ-cosecθ)[sin2 θ + cos2 θ-2 sinθ cosθ-1]
= (secθ -cosecθ)[1-2 sinθ cosθ-1]
= (secθ -cosecθ)[-2 sinθ cosθ]
= secθ[-2 sinθ cosθ ] – cosecθ[-2 sinθ cosθ]
= 1/cosθ [-2 sinθ cosθ]+1/sinθ [2 sinθ cosθ]
= -2[sinθ-cosθ ]
= -2p
23. [(1+ 2 sin A cos A)/(cos A + sin A) ] sec A =
(a)1+sec A
(b) 1-sec A
(c) 1+tan A
(d)1-tan A
Answer
Answer: (c) 1+tan A
Explanation: [(1+ 2 sin A cos A)/(cos A + sin A) ] sec A =
(cos2 A + sin2 A +2 sin A cos A )/(cos A +sin A )sec A
=[(cos A +sin A )2/(cos A +sin A) ] × (1/cos A)
= [cos A +sin A] × (1/cos A)
= (1 + sin A)/cos A
= 1 + tan A
24. (1+ cos A) (tan A+ cot A) – sec A cosec A =
(a)cosec A
(b) cos A
(c) sin A
(d) sec A
Answer
Answer: (a)cosec A
Explanation: (1+ cos A) (tan A+ cot A) – sec A cosec A =
(1+cos A)[sin A/cos A +cos A/sin A ] – sec A cosec A
= (1+cos A) [(sin2 A+ cos2 A)/cos A sin A] – sec A cosec A
= (1+cos A) [1/cos A sin A] – sec A cosec A
= 1/cos A sin A + cos A/cos A sin A – sec A cosec A
= sec A cosec A + cosec A -– sec A cosec A
= cosec A
25. If Sin A = cos A, then value of A is
(a)π/2
(b)π/4
(c)π/3
(d)π/6
Answer
Answer: (b)π/4
Explanation: Sin A = Sin π/4
=1/(√2)
= cos A
= cosπ/4
A = π/4
26. 8-8cos2 θ will be equal to
(a) cos2 θ
(b) 8 cos2 θ
(c) sin2 θ
(d)8 sin2 θ
Answer
Answer: (d)8 sin2 θ
Explanation: We know
sin2 θ + cos2 θ =1
8 (sin2 θ + cos2 θ) =1(8)
8 sin2 θ + 8 cos2 θ =8
8-8cos2 θ= 8 sin2 θ
27. If A=60, then (1- cos A)/(1+ cos A) =
(a) 1/3
(b)1/6
(c) 1/2
(d) 2/3
Answer
Answer: (a) 1/3
Explanation: (1-cosA)/(1+cosA )
= (1-cos60)/(1+cos60 )
=(1-1/2)/(1+1/2)
=(1/2)/(3/2)
= 1/3
28. If cos A + cos2A =1, then sin A+(1-cot2A)×(1/cosec2A)
(a)sin A-cos A
(b)sin A + cos A
(c) cos A – sin A
(d) None of these
Answer
Answer: (d) None of these
Explanation: cos A + cos2 θ =1
1-cos2 θ =cos A………………(a)
sin A+(1-cot2A)×(1/cosec2A)
= sin A + (1-(cos2 A)/(sin2 A))× 1/(1/(sin2 A))
= Sin A + (sin2 A – cos2 A)
= Sin A + (1 – cos2 A – cos2 A)
= Sin A + Cos A – cos2 A
29. If tan A = 1, then value of cosec A is
(a)1
(b)0
(c)√2
(d)√3
Answer
Answer: (c)√2
Explanation: tan A = tan π/4
A = π/4
Cosec A = cosec π/4
= √2
30. cos2A + cos2A sin2A =
(a) cos4A
(b) sin4A
(c) 1-cos4A
(d) None of these
Answer
Answer: (a) cos4A
Explanation: sin2 A + cos2 A =1
1-sin2 A = cos2 A
cos2 A+ cos2 A sin2 A = cos2 A [ 1 + sin2 A]
= [ 1 – sin2 A] [ 1 + sin2 A]
= 1 – sin4 A ∴[1-sin4 A =cos4 A]
= cos4 A
MCQ Questions for Class 10 Maths
- Real Numbers Class 10 MCQ with Answers
- Polynomials Class 10 MCQ with Answers
- Pair of Linear Equations in Two Variables
- MCQ Questions on Quadratic Equations for Class 10
- Arithmetic Progressions
- Triangles Class 10 MCQ with Answers
- Coordinate Geometry
- Introduction to Trignometry
- Some Applications of Trigonometry Class 10 MCQ with Answers
- Circles Class 10 MCQ with Answers
- Constructions Class 10 MCQ with Answers
- Areas Related to Circles
- Surface Areas and Volumes
- Statistics Class 10 MCQ with Answers
- Probability Class 10 MCQ
Frequently Asked Questions on Introduction to Trigonometry Class 10 MCQ with Answers
1. Are these MCQ on Introduction to Trigonometry Class 10 are based on 2021-22 CBSE Syllabus?
Yes . There are 30 MCQ’s on this Chapter in this blog.
2. Are you giving all the chapters of Maths Class 10 MCQs with Answers which are given in CBSE syllabus for 2021-22 ?
Yes, we are providing all the chapters of Maths Class 10 MCQs with Answers.