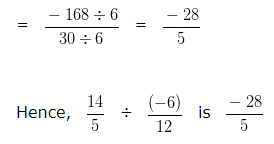In order to divide a Rational Number by another Rational Number
We have to multiply first Rational Number with Reciprocal of the second Rational Number.
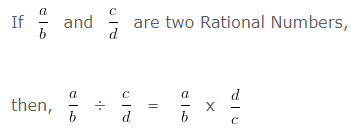
Dividing Rational Numbers Examples
Example 1
Divide:
9/7 ÷ 3/4
Explanation
We have, 9/7 ÷ 3/4
In order to divide a Rational Number by another Rational Number
We have to multiply first Rational Number with Reciprocal of the second Rational Number.
We have 9/7 ÷ 3/4
(Reciprocal of 3/4 is 4/3 )
So we can say that,
9/7 ÷ 3/4
= 9/7 x 4/3
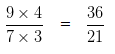
To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 36 and 21 is 3
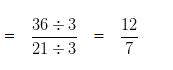
Dividing Rational Numbers Example 2
Divide:
14/5 ÷ -6/12
Explanation
We have, 14/5 ÷ 6/12
In order to divide a Rational Number by another Rational Number
We have to multiply first Rational Number with Reciprocal of the second Rational Number
Since, Reciprocal of -6/12 is 12/-6
We can write the given equation as 14/5 ÷ -6/12
= 14/5 x 12/-6
To make the Denominator positive, we would multiply 12 and -6 by -1
Given equation would now be 14/5 x -12/6
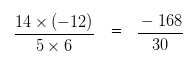
To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 168 and 30 is 6