Comparing Ratios – To Compare two Ratios, we should follow the following steps : –
- Write both the Ratios as Fractions
- Convert both the Fractions into Like Fraction:-
– Find the L.C.M of denominator of both the Fractions
– Make the denominator of each fraction equal to their L.C.M. - In case of Like fractions, the number whose numerator is greater is larger.
Comparing Ratios – Example 1
Compare the ratios ( 3 : 5 ) and ( 4 : 7 )
Explanation
We can write
( 3 : 5 ) = 3/5 and ( 4 : 7 ) = 4/7
Now, let us compare 3/5 and 4/7
LCM of 5 and 7 is 35
Making the denominator of each fraction equal to 35
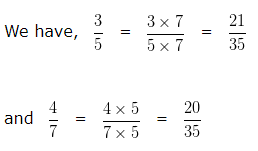
In case of Like fractions, the number whose numerator is greater is larger.
Hence we can say 21/35 > 20/35
That is, 3/5 > 4/7
Hence, ( 3 : 5 ) > ( 4 : 7 )
Comparing Ratios – Example 2
Compare the ratios ( 1 : 5 ) and ( 2 : 7 )
Explanation
We can write
( 1 : 5 ) = 1/5 and ( 2 : 7 ) = 2/7
Now, let us compare 1/5 and 2/7
LCM of 5 and 7 is 35
Making the denominator of each fraction equal to 35
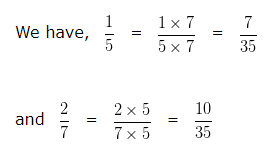
In case of Like fractions, the number whose numerator is greater is larger.
Hence we can say 7/35 < 10/35
That is, 1/5 < 2/7
Hence, ( 1 : 5 ) < ( 2 : 7 )
Comparing Ratios – Example 3
Compare the ratios ( 7 : 4 ) and ( 6 : 8 )
Explanation
We can write
( 7 : 4 ) = 7/4 and ( 6 : 8 ) = 6/8
Now, let us compare 7/4 and 6/8
LCM of 4 and 8 is 8
Making the denominator of each fraction equal to 8
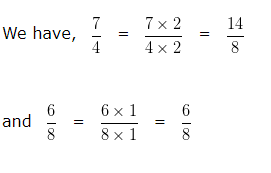
In case of Like fractions, the number whose numerator is greater is larger.
Hence we can say 14/8 > 6/8
That is 7/4 > 6/8
Hence, ( 7 : 4 ) > ( 6 : 8 )
Comparing Ratios – Example 4
Compare the ratios ( 3 : 4 ) and ( 2 : 3 )
Explanation
We can write
( 3 : 4 ) = 3/4 and ( 2 : 3 ) = 2/3
Now, let us compare 3/4 and 2/3
LCM of 4 and 3 is 12
Making the denominator of each fraction equal to 12
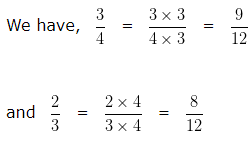
In case of Like fractions, the number whose numerator is greater is larger.
Hence we can say 9/12 > 8/12
That is 3/4 > 2/3
Hence, ( 3 : 4 ) > ( 2 : 3 )
Comparing Ratios – Example 5
Compare the ratios ( 1 : 5 ) and ( 1 : 4 )
Explanation
We can write
( 1 : 5 ) = 1/5 and ( 1 : 4 ) = 1/4
Now, let us compare 1/5 and 1/4
LCM of 5 and 4 is 20
Making the denominator of each fraction equal to 20
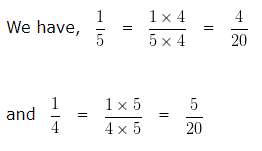
In case of Like fractions, the number whose numerator is greater is larger.
Hence we can say 4/20 < 5/20
That is, 1/5 < 1/4
Hence, ( 1 : 5 ) < ( 1 : 4 )