A body which is in motion possesses some speed. This speed can be constant or may be changing. Further, it may be changing uniformly, with equal amounts in equal intervals of time or non-uniformly, with unequal amounts in equal intervals of time. The moving body can cover different parts of its distance in many different speeds. Here is where average speed and average velocity comes into discussion.
The concept of average speed or average velocity comes in use when a body covers the distance with different speeds. In such cases it is difficult to explain the motion of the object. Hence, terms such as average speed and velocity are used to interpret the motion and analyse the various parameters involved with it.
Let us start looking at these terms one by one.
Average speed
The average speed of a body is the total distance travelled divided by the total time taken to cover this distance. While travelling in a car or bus we have noticed that it is very difficult to keep the speed of the car at a constant or uniform value because at many places the brakes are to be applied to slow down or stop the car due to various reasons. Thus, the speed of a body is usually not constant and the distance travelled divided by time gives us the average speed during that time. For example, for a car which travels a distance of 100 km in 4 hours, the average speed is 100/4 = 25 km per hour. Although the average speed of this car is 25 km per hour, it does not mean that the car is moving at this speed all the time. When the road is straight, flat and free, the speed may be much more than 25 km per hour but on bends (curved road), hills or in a crowded area, the speed may fall well below this average value. We should remember that:
Average Speed = Total distance travelled/ Total time taken
We will use this formula for solving numerical problems after a while.
Average velocity
The average velocity of a body is the total displacement of the body divided by the total time taken to cover that displacement.
Average Velocity = Total displacement/total time
If the velocity of a body is always changing, but changing at a uniform rate (the acceleration is uniform), then the average velocity is given by the “arithmetic mean” of the initial velocity and final velocity for a given period of time, that is:
Average Velocity = (Initial velocity + Final velocity)/2
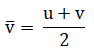
Where v bar (written as ‾v‾ ) denotes the average velocity, u is the initial velocity and v is the final velocity. This formula for calculating the average velocity will be helpful in solving the numerical problems, so it should be memorised.
Example –
A car travels 30 km at a uniform speed of 40 km/h and the next 30 km at a uniform speed of 20 km/h. Find its average speed.
Solution –
Total distance travelled = (30+30) km = 60 km
Time taken to cover first 30 km = Distance Covered/Speed at which distance is covered
30/40 = hours = 0.75 hours
Time taken to cover next 30 km = Distance Covered/Speed at which distance is covered
30/20 = hours = 1.5 hours
Total time taken = 2.25 hours
Average speed = Total distance travelled/Total time taken = 60/2.25 = 26.6 km/h
Questions related to the topic Average speed and Average velocity from NCERT textbook –
Page 112 and 113
Question 2 – Average Speed and Average Velocity
Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging:
- From A to B?
- From A to C?
Solution –

- Total distance from A to B = 300 m
Total time taken from A to B = 2 minutes 30 seconds
= 2×60 seconds + 30 seconds
= 150 s
Average Speed = Total distance/Total time
= 300m/150s = 2 m/s
Total displacement from A to B = 300 m
Total time taken from A to B = 150 s
Average velocity = Total displacement/Total time
= 300m/150s = 2 m/s
- Total distance from A to B to C = (300+100)m = 400m
Total time taken= 2 minute 30 seconds + 1 minute
= 150 seconds + 60 seconds
= 210 seconds
Average Speed = Total distance/Total time
= 400m/210s = 1.9 m/s
Displacement from A to B to C = (300-100) m
= 200 m
Total time taken = 210 s
Average velocity = Displacement/Total time
= 200m/210s
= 0.95 m/s
Question 3 – Average Speed and Average Velocity
Abdul, while driving to school, computes the average speed for his trip to be 20 km/h. on his return trip along the same route, there is less traffic and the average speed is 30 km/h. What is the average speed for Abdul’s trip?
Solution –
Suppose that the school is at a distance ‘x’ of km.
Suppose the time taken to drive to school is t1. The average speed of this trip is 20 km/h.
Speed = Distance/Time
20 = x/t1
Time taken, t1 = (x/20) h
Suppose that the time taken to drive from school is t2. The average speed of this trip is 30 km/h.
Speed = Distance/Time
30 = x/t1
Time taken, t2 = (x/30)h
Total distance for whole trip = x + x = 2x km
Total time taken = (x/20) + (x/30)
= (3x+2x)/60
= 5x/60
= (x/12) h
Average speed = Total distance covered/total time taken
= (2x × 12)/x
= 24 km/h
Conclusion – The terms such as average speed and average velocity are used to describe the motion of a body that moves with different speeds in different parts of its motion. For example, the motion of a car moving on a road full of traffic is non-uniform so its average speed will help to interpret its motion very well.Average speed is the total distance travelled by the body divided by the total time taken to travel that distance. Average velocity is the total displacement divided by the total time taken to cover that displacement.