Arithmetic Progression Class 10 Maths, deals with various concepts which are as under:-
- Arithmetic Progressions
- nth Term of an AP
- Sum of First n Terms of an AP
1. Arithmetic Progression
Introduction of Arithmetic Progression, First term and Common Difference
Arithmetic Progression is a series of numbers, in which each successive termis obtained by adding a fixed number to the preceding term except the first term. that fixed term is known as common difference, which can be positive or negative.
2. nth term of an AP – Arithmetic Progression Class 10
If 1st term = a
Common difference = d
we know that for an AP
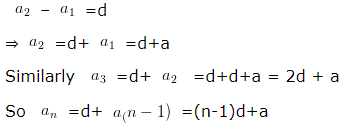
Finding first 5 terms of an Arithmetic Progression when first term and common difference are given?
Determining whether given data forms an AP?
Find Common Difference – 1st and 6th term of Arithmetic Progression given
Finding the missing terms of an Arithmetic Progression
Find ranking of a term in an Arithmetic Progression
First negative term in an Arithmetic Progression
Number of multiples of given number in Arithmetic Progression
Finding the salary in Year 10 Arithmetic Progression
Correlation between terms of an Arithmetic Progression given – Finding AP
3. Sum of n terms of an AP – Arithmetic Progression Class 10
a + (a + d) + (a + 2d) + (a + 3d)…………. + (a + (n – 1)d) = S ……………………. (1)
(a + (n – 1)d) + ……………………………+ (a + d) + a = S ……………………………….(2)
Add equation 1 and 2. We will get
2S = n{2a + (n – 1)d}
S = Sum of n terms of an AP = n/2{2a+(n-1)d}
Sum of an Arithmetic Progression
Finding Sum of Arithmetic Progression upto given number of terms
1st and last term of Arithmetic Progression and Sum thereof
Sum of n terms of an AP = n/2 {2a+(n-1)d}=n/2 {a+a+(n-1)d}=n/2{a+an}
Because we know that nth term of AP = a + (n – 1)d
nth term of an AP = Difference between the sum of n terms and sum of (n – 1)terms
![]()
Total Cost of tractor including interest – Arithmetic Progression problem 1