Area Related to Circles Class 10 MCQ Questions are covered in this Article. Area Related to Circles Class 10 MCQ Test contains 30 questions. Answers to MCQs on Area Related to Circles Class 10 Maths are available at the end of the last question. MCQ Questions for Class 10 Maths with Answers have been made for Class 10 students to help check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Board | CBSE |
| Textbook | Maths (NCERT) |
| Class | Class 10 |
| Chapter | Chapter 12 Area Related to Circles |
| Category | MCQ Questions for Class 10 Maths with Answers |
Area Related to Circles Class 10 MCQ Questions
1. 2πr of a circle is:
(a) Circumference
(b) Area
(c) Diameter
(d) segment
Answer
Answer: (a) Circumference
2. The value of π is
(a) 3.41
(b) 2.14
(c) 3.14
(d) 4.13
Answer
Answer: (c) 3.14
Explanation: π = 22/7 = 3.14
3. What is the relation of diameter with initial radius, if the radius of a circle is reduced by one fourth?
(a) d = 2r
(b) d = r/4
(c) d = 4r
(d) d = r/2
Answer
Answer: (d) d = r/2
Explanation: r2 = r1 /4
d =2 × r2
= 2 × r1/4
= r1/ 2
4. The circumference of a circle is
(a) Linear distance around the circle
(b) Length of complete arc of the circle
(c) Both
(d) None of the above
Answer
Answer: (c) Both
5. Odd one out
(a) Radius
(b) Diameter
(c) circumference
(d) diagonal
Answer
Answer: (d) diagonal
6. Find the area of the circle, when its circumference is 44cm.
(a) 144cm2
(b) 154cm2
(c) 44cm2
(d) 220cm2
Answer
Answer: (b) 154cm2
Explanation: Circumference = 2πr
44 = 2πr
r = 22 / π
Area = πr2 = π × 22/π × 22/π = 22 × 7 = 154cm2
7. Swapnil is celebrating his birthday with his four friends. The cake is circular in shape with radius 2.8cm. He cut the cake and distributed its equal parts among his friends. Find the area of the cake he distributed to each friend.
(a) 6.16 cm2
(b) 6.10 cm2
(c) 16.6 cm2
(d) 6.20 cm2
Answer
Answer: (a) 6.16 cm2
Explanation:
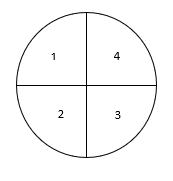
Angle at center = 360˚
Angle of sector of circle = 360 / 4 = 90˚
Area of the cake he distributed to each friend
= Area of sector of a circle
= θ/(360˚) x πr2
= (90˚)/(360˚) x 22/7 x 2.8 x 2.8
= 22 x 0.7 x 0.4= 6.16 cm2
Area Related to Circles Class 10 MCQ Questions
8. A part of a circle made of the arc of the circle along with its two radii is called as
(a) Circumference
(b) Sector
(c) Segment
(d) Area
Answer
Answer: (b) Sector
9. A region bounded by a chord of a circle and the intercepted arc of the circle is
(a) Circumference
(b) Sector
(c) Segment
(d) Area
Answer
Answer: (c) Segment
10. The circumference of a circle of area 5π cm2 is
(a) √5π cm
(b) 6π cm
(c) 2√5 cm
(d) 2√5π cm
Answer
Answer: (d) 2√5π cm
Explanation:
Area of circle = πr2
5π = πr2
r = √5 cm
Circumference of circle = 2πr = 2√5π cm
11. Two circles with the centers O and O’ touching each other internally at center . Find the ratios of their areas.
(a) 3:2
(b) 4:1
(c) 3:4
(d) 1:1
Answer
Answer: (b) 4:1
Explanation:
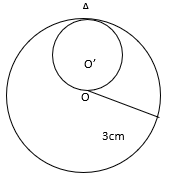
In larger circle, Area1 = πr² = π x 3 x3 = 9πcm²
In smaller circle, diameter = radius of larger circle = 3cm
Radius = 3 /2 = 1.5cm
Area2 = π x 1.5 x 1.5 = 2.25πcm²
A1: A2 = 9π: 2.25π = 4:1
12. Name 1 and 2 given in the figure
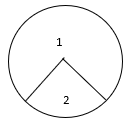
(a) Minor sector and major sector
(b) Major sector and minor sector
(c) Minor segment and major segment
(d) Major segment and minor segment
Answer
Answer: (b) Major sector and minor sector
13. Find the area of segment
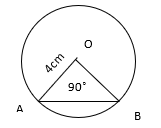
(a) 4.16cm2
(b) 14.6cm2
(c) 4.56cm2
(d) 4.78cm2
Answer
Answer: (c) 4.56cm2
Explanation:
Area of segment = Area of sector – Area of triangle
Area of sector = θ/(360˚) × πr2
= (90˚)/(360˚) × 22/7 × 4 × 4
= (3.14 × 4) cm2
= 12.56 cm2
Area of triangle AOB = 1/2 × base × height = 1/2 × 4×4 = 8cm2
(It is a right-angled triangle, ∠O = 90˚)
Area of segment = 12.56 – 8 = 4.56cm2
14. Find the perimeter of a circle, inscribing in a square of side 14cm.
(a) 44cm
(b) 65cm
(c) 40cm
(d) 52cm
Answer
Answer: (a) 44cm
Explanation:
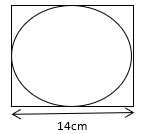
Diameter of circle = side of square = 14cm
Radius = 14/2 = 7cm
Perimeter of circle = 2πr
= 2 × 22/7 × 7
= 44cm
15. How many sectors can you draw in the circle having 60˚ angle at center.
(a) 3
(b) 4
(c) 5
(d) 6
Answer
Answer: (d) 6
Explanation: There will be exactly 6 sectors in a circle having 60˚ angle at center.
Angle at the center of circle = 360˚
For 6 sectors = 360 /6 = 60˚ angle at center.
16. The ratio of the perimeters of the two circles in the figure is
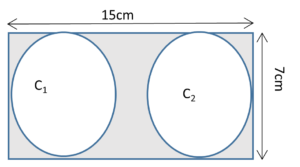
(a) 1:1
(b) 1:2
(c) 1:3
(d) 1:4
Answer
Answer: (a) 1:1
Explanation:
diameter of both circles = breath of rectangle = 7cm
Radius of both circles = 7/2 = 3.5cm
Perimeter of C1: Perimeter of C2
= 2πr1: 2πr2
= r1: r2
= 3.5: 3.5
= 1:1
17. A line segment extending from the center of a circle to the circumference is
(a) Chord
(b) Tangent
(c) Radius
(d) Diameter
Answer
Answer: (c) Radius
18. Find the area of shaded region.
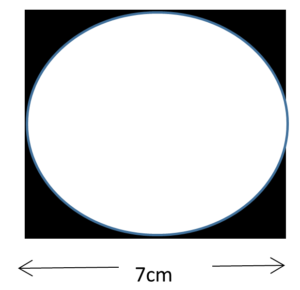
(a) 10.4cm2
(b) 10.5cm2
(c) 6.7cm2
(d) 7.2 cm2
Answer
Answer: (b) 10.5cm2
Explanation:
diameter of circle = side of square = 7cm
Radius = 7 /2 = 3.5cm
Area of shaded region = area of square – area of circle
= side × side – πr2
= 7 ×7 – 22/7 × 3.5 × 3.5
= 49 – 38.5 = 10.5cm2
Area Related to Circles Class 10 MCQ Questions
19. If the area of circle is equal to its perimeter, find the radius of circle.
(a) 2
(b) 3
(c) 4
(d) 6
Answer
Answer: (a) 2
Explanation: Area of circle = Circumference of circle
πr2 = 2πr
r = 2
20. Any straight line drawn from the edge of a circle to another edge and passes through the center of the circle is
(a) Chord
(b) Tangent
(c) Radius
(d) Diameter
Answer
Answer: (d) Diameter
21. The line segment that joins two distinct points of a circle is
(a) Secant
(b) Tangent
(c) Chord
(d) Diameter
Answer
Answer: (c) Chord
22. As shown in figure, a circle is inscribed in a square of side 4cm. Find the length of an arc of a sector of the circle.
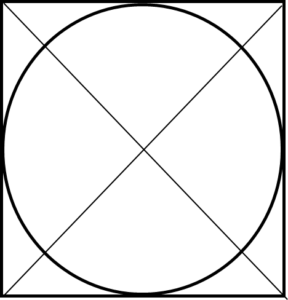
(a) 6cm
(b) 3.14cm
(c) 12.56cm
(d) None
Answer
Answer: (b) 3.14cm
Explanation: The diagonals of a square are equal and bisect each other at right angles. So, angle of sector of the circle = 90˚
Diameter of circle = side of square = 4cm
Radius = 4/2 = 2cm
Length of arc of sector of 90˚ = θ/(360˚) × 2πr
= (90˚)/(360˚) × 2 × 22/7 × 2
= 3.14 cm
23. Find the area of major sector of the circle of radius 7cm.
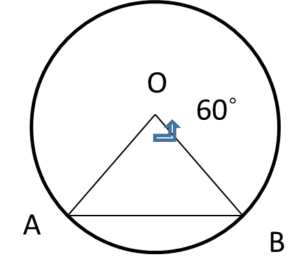
(a) 149 cm2
(b) 70 cm2
(c) 128.33 cm2
(d) 128 cm2
Answer
Answer: (c) 128.33 cm2
Explanation: Area of major sector = (360˚ – θ)/(360˚) × πr2
= (360˚ – 60˚)/(360˚) × 22/7 × 7× 7
= (300˚)/(360˚) × 154
= 128.33cm2
24. Find the area of shaded region in the circle of radius 6cm and 3cm and having an angle of sector 60˚
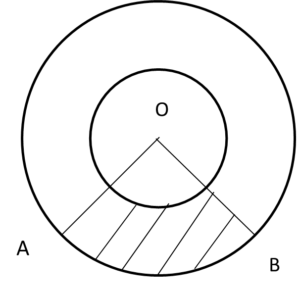
(a) 1.56π
(b) 4.5π
(c) 5π
(d) 9π
Answer
Answer: (b) 4.5π
Explanation: ∠AOB = 60°
Area of sector of big circle = A2 = ( θ)/(360˚) × πr²
= ( 60˚)/(360˚) × π × 6 × 6 = 6π
Area of sector of small circle = A1 = ( θ)/(360˚) × πr²
= ( 60˚)/(360˚) × π × 3 × 3 = 1.5π
Area of shaded region = A2 – A1
= 6π – 1.5π = 4.5π
Area Related to Circles Class 10 MCQ Questions
25. A circle is drawn from one of the vertices of square of side 5cm. Find the area of shaded region.
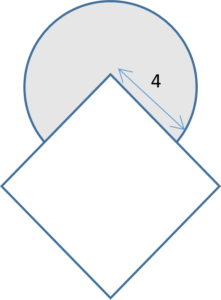
(a) 37cm2
(b) 25cm2
(c) 50cm2
(d) None of the above
Answer
Answer: (d) None of the above
Explanation: In a square, all the sides are equal and each
angle is equal to 90˚
Angle of sector = 90˚
Area of shaded region = Area of major sector
= (360˚ – θ)/(360˚) × πr²
= (360˚ – 90˚)/(360˚) × π × 4 × 4
= (270˚ )/(360˚) × 22/7 × 4 × 4
= 37.7cm²
26. The circumference of a circle is equal to area of square of side πcm. Find the ratio of radius of circle to side of square.
(a) 1:2
(b) 2:1
(c) π: 2
(d) 2: π
Answer
Answer: (a) 1:2
Explanation: circumference of a circle = area of square
2πr = side × side
2πr = π × π
r = π /2
r: π = 1:2
27. A sector of a circle of angle 270˚ is inscribed in a square of side 8cm. Find the area of shaded region.
(a) 26cm2
(b) 32cm2
(c) 32cm2
(d) 64cm2
Answer
Answer: (c) 32cm2
Explanation:
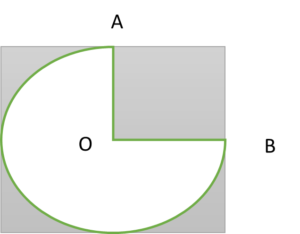
Area of shaded region = Area of square – area of major sector
Radius of circle = d/2
= 8/2 = 4cm
Area of major sector = ( θ)/(360˚) × πr²
= ( 270˚)/(360˚) × π × 4 × 4
= 12π = 37.68cm²
Area of square = side × side
= 8 ×8 = 64cm²
Area of shaded region = 64 – 37.68
= 26.32cm²
28. Find the length of arc of sector of a circle with 60˚ angle and 21cm of radius.
(a) 21cm
(b) 22cm
(c) 42cm
(d) 44cm
Answer
Answer: (b) 22cm
Explanation: Length of arc of sector of 60˚ = θ/(360˚) × 2πr
= (60˚)/(360˚) × 2 × 22/7 × 21
= 22 cm
29. Find the area of semi- circle, where circumference of circle is 22cm.
(a) 220cm2
(b) 420cm2
(c) 300cm2
(d) 19.25cm2
Answer
Answer: (d) 19.25cm2
Explanation:
Circumference = 2πr
22 = 2× 22/7 × r
r = 7/2cm
= 3.5 cm
Area of semi circle = πr² / 2
= 22/7 × (3.5×3.5)/2
=19.25cm²
30. The perimeter of a sector of circle with radius 14cm is 22cm. Find the area of sector.
(a) 154cm2
(b) 220cm2
(c) 440cm2
(d) 200cm2
Answer
Answer: (a) 154cm2
Explanation:
Length of arc of sector = θ/(360˚) × 2πr
22 = θ/(360˚) × 2 × 22/7 × 14
θ = 90˚
Area of sector = θ/(360˚) × πr²
= (90˚)/(360˚) × 22/7 x 14 x 14
= 154cm²
MCQ Questions for Class 10 Maths
- Real Numbers Class 10 MCQ with Answers
- Polynomials Class 10 MCQ with Answers
- Pair of Linear Equations in Two Variables
- MCQ Questions on Quadratic Equations for Class 10
- Arithmetic Progressions
- Triangles Class 10 MCQ with Answers
- Coordinate Geometry
- Introduction to Trignometry
- Some Applications of Trigonometry Class 10 MCQ with Answers
- Circles Class 10 MCQ with Answers
- Constructions Class 10 MCQ with Answers
- Areas Related to Circles
- Surface Areas and Volumes
- Statistics Class 10 MCQ with Answers
- Probability Class 10 MCQ