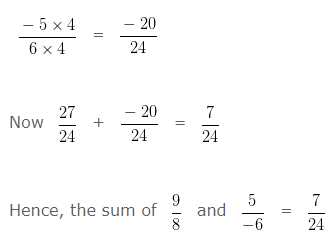Addition of Rational Numbers, deals with various concepts which are as under:-
- Addition of Rational Numbers When Denominator Are Equal
- Addition of Rational Numbers When Denominators Are Unequal
When we have to add two rational numbers, First we should convert each of them into a rational number with a positive denominator.
Addition of Rational Numbers When Denominator Are Equal
Question 1
Find the sum of 5/9 and -4/9
Explanation
Sum of Rational Numbers whose Denominators are equal

Question 2
Find the sum of 19/13 and 11/(-13)
Explanation
To add two Rational Numbers, first their Denominators should be positive
So, we would first express 11/(-13) as a Rational Number with a positive Denominator.
Multiplying both the Numerator and Denominator by (-1)

Addition of Rational Numbers When Denominators Are Unequal
Question 3
Find the sum of 7/6 and 5/9?
Explanation
To add two Rational Numbers with different Denominator, we will first find the LCM of both the Denominators.
LCM of 6 and 9 is 18
Now we would divide such LCM by Denominator of first number and the result would be multiplied with both the numerator and denominator of such number
Dividing LCM by the Denominator of first number
18 ÷ 6 = 3
Multiplying both the Numerator and Denominator of 7/6 by the quotient i.e, 3
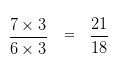
Dividing LCM by the Denominator of Second number
18 ÷ 9 = 2
Multiplying both the Numerator and Denominator of 5/9 by 2
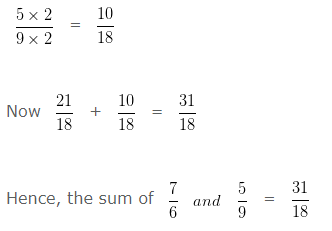
Question 4
Find the sum of 9/8 and 5/(-6)?
Explanation
To add two Rational Numbers, first their Denominators should be positive
So, we would first express 5/(-6) as a Rational Number with positive Denominator.
Multiplying both the Numerator and Denominator by (-1)
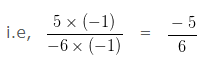
To add two Rational Numbers with different Denominator first we will find the LCM of both the Denominators.
LCM of 8 and 6 is 24
Divide LCM by the Denominator of first number
24 ÷ 8 = 3
We have to multiply , both the Numerator and Denominator of 9/8 by the quotient i.e, 3
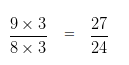
Divide LCM by the Denominator of second number
24 ÷ 6 = 4
We have to multiply , both the Numerator and Denominator of -5/6 by 4