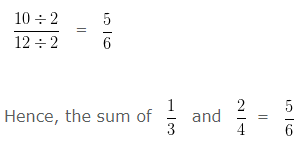Addition of Like Fractions | Addition of Unlike Fractions

Addition of Like Fractions and Addition of Unlike Fractions

To add Like Fractions, we add the numerators and write the sum over the same denominator.

To add Unlike Fractions, first we have to change the Unlike Fractions, into equivalent Like Fractions, and then add the two equivalent Like Fractions

Example on Addition of Like Fractions

Addition of like Fraction – Example 1

Find the sum of 5/12 and 1/12 and reduce to its lowest term.

Explanation:

On Simplifying further,

HCF of 6 and 12 is 6

Dividing both Numerator and Denominator by their HCF i.e, 6

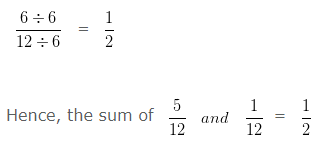
Addition of like Fraction – Example 2

Find the sum of 3/6 and 5/6 and reduce to its lowest term.

Explanation:

On Simplifying further,

HCF of 8 and 6 is 2

Dividing both Numerator and Denominator by their HCF i.e,

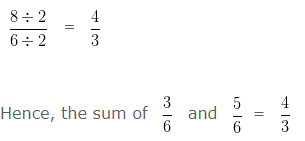
Example on Addition of Unlike Fractions

Addition of Unlike Fraction – Example 1:

Find the sum of 5/12 and 2/6 and reduce to its lowest term.

Explanation:

In order to add Unlike Fraction

Firstly, we have to change the Unlike Fraction, into equivalent Like Fractions, and then add the two equivalent Like Fractions

LCM of 12 and 6 is 12

Converting the Unlike Fraction into Equivalent Like Fraction

On Simplifying further,

HCF of 9 and 12 is 3

Dividing both Numerator and Denominator by their HCF i.e, 3

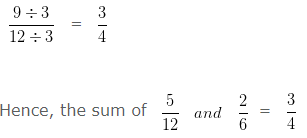
Addition of Unlike Fraction – Example 2:

Find the sum of 1/3 and 2/4 and reduce to its lowest term.

Explanation:

In order to add Unlike Fraction

Firstly, we have to change the Unlike Fraction, into equivalent Like Fractions, and then add the two equivalent Like Fractions

Take LCM of 3 and 4 is 12

Converting the Unlike Fraction into Equivalent Like Fraction

On Simplifying further,

HCF of 10 and 12 is 2

Dividing both Numerator and Denominator by their HCF i.e,