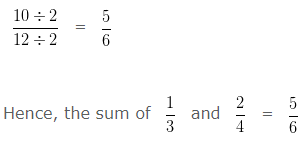Adding Fractions

Adding Fractions (Addition of Fractions), deals with various concepts which are as under:-

• Adding Fractions with same Denominators ( Like Fractions )
• Adding Fractions with different Denominators ( Unlike Fractions )

To add Fractions with same denominators ( Like Fractions ), we add the numerators and write the sum over the same denominator.

To add Fractions with different denominators ( Unlike Fractions ), first we have to change the Unlike Fractions, into equivalent Like Fractions, and then add the two equivalent Like Fractions

Adding Fractions with same Denominators ( Like Fractions )

Example 1

Find the sum of 5/12 and 1/12 and reduce to its lowest term.

Solution

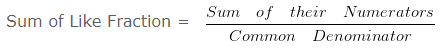
Sum of Like Fraction = (5+1)/12

Sum of Like Fraction = 6/12

Hence, the sum of 5/12 and 1/12 is 6/12.

Simplifying further,
HCF of 6 and 12 is 6
Dividing both Numerator and Denominator by their HCF i.e,

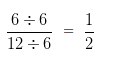
Hence, the sum of 5/12 and 1/12 = 1/2

Example 2

Find the sum of 3/6 and 5/6 and reduce to its lowest term.

Solution

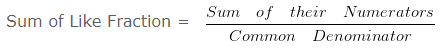
Sum of Like Fraction = (3+5)/6

Sum of Like Fraction = 8/6

Hence, the sum of 3/6 and 5/6 is 8/6

Simplifying further,
HCF of 8 and 6 is 2
Dividing both Numerator and Denominator by their HCF i.e,

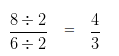
Hence, the sum of 3/6 and 5/6 = 4/3

Adding Fractions with different Denominators ( Unlike Fractions )

Example 1

Find the sum of 5/12 and 2/6 and reduce to its lowest term.

Solution

In order to add Unlike Fraction

Firstly, we have to change the Unlike Fraction, into equivalent Like Fractions, and then add the two equivalent Like Fractions

Take LCM of 12 and 6 is 12

Converting the Unlike Fraction into Equivalent Like Fraction

Simplifying further,
HCF of 9 and 12 is 3
Dividing both Numerator and Denominator by their HCF i.e,

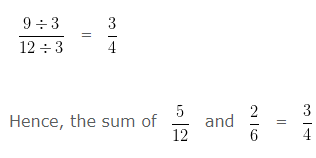
Example 2

Find the sum of 1/3 and 2/4 and reduce to its lowest term.

Solution

In order to add Unlike Fraction
Firstly, we have to change the Unlike Fraction, into equivalent Like Fractions, and then add the two equivalent Like Fractions

Take LCM of 3 and 4 is 12

Converting the Unlike Fraction into Equivalent Like Fraction

Simplifying further,
HCF of 10 and 12 is 2
Dividing both Numerator and Denominator by their HCF i.e,