Lets learn about the Acute Angled triangle (AAT), Right Angle Triangle (RAT) and Obtuse Angled Triangle in this Post
Acute Angled Triangle
When all the Angles of a Triangle are less than 90°, we call such a triangle as an AAT .
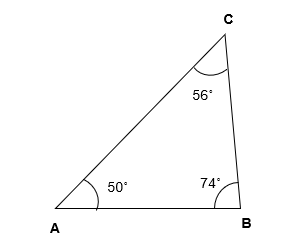
For Example – ∆ ABC is an AAT as all the three angles i.e, ∠BAC, ∠ACB and ∠ABC are less than 90° (Acute Angle).
Right Angled Triangle – RAT
When one angle of a triangle is 90° and the other two angles are acute ( less than 90°) then we call such a triangle as a RAT.
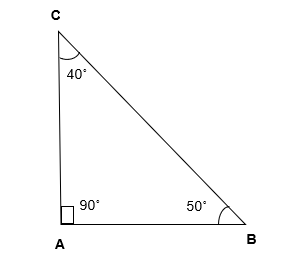
For Example – In ∆ ABC ∠BAC is 90° ( right angle ) and ∠ACB and ∠ABC are less than 90° ( acute angle ).
Obtuse angled triangle
If one angle of a triangle is obtuse ( greater than 90°) and other two are acute ( less than 90°), we call such a triangle as Obtuse angled triangle.
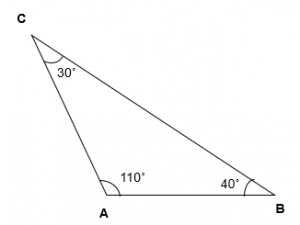
For Example – ∆ABC is an Obtuse Angled triangle as ∠BAC is 110° (obtuse angle) and ∠ACB and ∠ABC are acute angle (less than 90°).
EXAMPLE 1
If the measure of the angle of the triangle are 56 ˚ , 49 ˚ and 75 ˚, then the triangle is —- Triangle ?
EXPLANATION
Here,
56 ˚ < 90 ˚
49 ˚ < 90 ˚
75 ˚ < 90 ˚
Since, all the three angles of triangle are less than 90˚, hence, the triangle is An AAT.
EXAMPLE 2
If the measure of the angle of the triangle are 90 ˚ , 54 ˚ and 36 ˚, then the triangle is?
EXPLANATION
Here,
90 ˚ = 90 ˚
54 ˚ < 90 ˚
36 ˚ < 90 ˚
Since, one angle is 90˚ and the other two angles are acute angle (less than 90˚, hence, the triangle is a Right Angled Triangle.
EXAMPLE 3
If the measure of the angle of the triangle are 93 ˚ , 55 ˚ and 32 ˚, then the triangle is?
EXPLANATION
Here,
93 ˚ > 90 ˚
55 ˚ < 90 ˚
32 ˚ < 90 ˚
Since, one angle of a triangle is obtuse ( greater than 90˚ ) and other two are acute angles (less than 90˚)
Hence, the triangle is an Obtuse Angled Triangle