Surface Area and Volume Class 9 MCQ – Maths Class 9 MCQ Online Test are covered in this Article. Surface Area and Volume Class 9 MCQ Test contains 29 questions. Answers to MCQ on Surface Area and Volume Class 9 are available after clicking on the answer. MCQ Questions for Class 9 with Answers have been made for Class 9 students to help check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Board | CBSE |
| Textbook | Maths (NCERT) |
| Class | Class 9 |
| Chapter | Chapter 13 Surface Area and Volume |
| Category | MCQ Questions for Class 9 Maths with Answers |
Surface Area and Volume Class 9 MCQ
1.Name the shapes in the figure
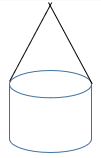
(a) Sphere + cylinder
(b) Triangle +circle +rectangle
(c) Cone + cylinder
(d) cylinder
Answer
Answer: (c) Cone + cylinder
2. Find the CSA of given figure

(a) 2πrh
(b) 2πr (r+ h)
(c) πr2h + 2π
(d) πr(2h+l)
Answer
Answer: (d) πr(2h+l)
Explanation:
TSA of given figure = CSA of cylinder+ CSA of cone
= 2πrh + π r l = πr (2h+l)
3. Volume of cone is…………
(a) (1/3)πr2h
(b) (4/3)πr2h
(c) 2πr2h
(d) (1/3)πrh
Answer
Answer: (a) (1/3)πr2h
4. Find TSA of a storage container.

(a) 2πrh
(b) 2π (r + l)
(c) 2π2(r + h)
(d) 2(l b + b h + hl)
Answer
Answer: (d) 2(l b + b h + hl)
Explanation: TSA of storage container = TSA of Cuboid = 2(l b + b h + hl)
5. Find the volume of unshaded region.
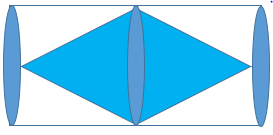
(a) Volume of Cuboid
(b) Volume of Cone
(c) Volume of cylinder
(d) Volume of Cube
Answer
Answer: (b) Volume of Cone
Explanation:
Volume of cylinder – 2(vol of cone)
= πr2h – 2 x 1/3πr2h
= πr2h (1 – 2/3 )
= 1/3πr2h = vol of cone
6. A cuboid whose length, breadth and height are all equals, then the shape obtained is
(a) Cylinder
(b) Cone
(c) Cube
(d) frustum
Answer
Answer: (c) Cube
Explanation: cube is a shape whose, l=b=h
7. If one solid is converted into another solid, then the volume of the new shape will
(a) Increase
(b) Decrease
(c) Same
(d) Doubled
Answer
Answer: (c) Same
Explanation: When one solid is converted into another solid, the volume of the new shape will remain same.
Surface Area and Volume Class 9 MCQ
8. A metallic hollow cone of height 6cm and internal and external diameters 6cm and 10cm respectively, is melted and recast into the form of a cylinder with diameter 8cm. The height of the cylinder is
(a) 1cm
(b) 2 cm
(c) 5 cm
(d) 6cm
Answer
Answer: (b) 2 cm
Explanation:
When one solid is converted into another solid, the volume of the new shape will remain same.
Volume of cylinder = volume of cone
π r2 h = 1/3 π (R2 – r2) h
π × 42 × h = 1/3 × π × (52 – 32) × 6
π × 16 × h = 1/3 × π × 16 × 6 => h = 2cm
9. A box is in a shape of cube measuring 10m. Find the no. Of sheets required to wrap the box, if a sheet measures 2m x 1.5m.
(a) 10
(b) 75
(c) 80
(d) 200
Answer
Answer: (d) 200
Explanation:
No. Of sheets = TSA of cubical box / area of sheet
= 6 × Side2 / l ×b (area of sheet= area of rectangle)
= (6 × 10 × 10)/(2 × 1.5) = 200
10. Find the volume of cylinder, if radius is doubled and height is halved.
(a) V1 = 2V2
(b) V2 = 2V1
(c) V1 = (2/3)V2
(d) V2 = (2/3)V1
Answer
Answer: (b) V2 = 2V1
Explanation: Vol of cylinder = π× r2× h
Here, r = 2r; h = h/2
Vol of cylinder = π × (2r)2× h/2
= π × 4r2× h/2 = 2 × π × r2 × h
11. Find the ratio of area of C1 and C2, where the height of smaller cone is exactly half of bigger cone.
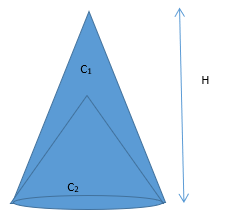
(a) √(r2+h2)/(2r2+h2)
(b) 2√(r2+h2)/(2r2+h2)
(c) √(2r2+h2)/(r2+h2)
(d) 2√(r2+h2)/(4r2+h2)
Answer
Answer: (d) 2√(r2+h2)/(4r2+h2)
Explanation: TSA of C1: TSA of C2
= πr1l1: πr2l2
= (π × r × √(r2 + h2) )/(π × r × √ (r2 + h2 ⁄(4 )))
= 2√(r2+h2)/(4r2+h2)
12. Find the radii of a sphere, when 10 solid spheres of same radii R are being made by melting a cylinder of radius 3cm and height 12cm.
(a) 2cm
(b) 3√3 cm
(c) 25cm
(d) 5√3 cm
Answer
Answer: (b) 3√3 cm
Explanation:
When one solid is converted into another solid, the volume of the new shape will remain same.
Volume of sphere = volume of cylinder
4/3 π r3 = πr2h
4× π × r3 = 3 × π × 3×3 × 12
R3 = 3×3×3×3
R = 3√3 cm
13. Volume of two spheres are in a ratio of 125:64. Find the ratio of its surface areas.
(a) 4/5
(b) 16/25
(c) 25/16
(d) None of the above
Answer
Answer: (c) 25/16
Explanation:
V1/ V2 = 125 /64
(1/3) π r13 / (1/3) π r23 = 125 /64
(r1 / r2)3 = 125 / 64
r1 / r2 = 5/4
S1 / S2 = 4π r12 / 4π r22
= (r1 / r2)2 = (5 / 4 )2 = 25/ 16
14. The diameter of the circular ends of a rod of height 21cm are 20cm. Find the volume of rod. (π = 22/7)
(a) 30000 cm3
(b) 45000 cm3
(c) 5600 cm3
(d) 6600cm3
Answer
Answer: (d) 6600cm3
Explanation:
A rod is in a shape of cylinder.
So, vol of rod = vol of cylinder = π r2 h
= 22/7 × 21 × 10 × 10= 6600cm3
15. Find the height of cuboid if length and breadth of it are 10cm and 15cm respectively, given that the lateral surface area of cuboid is 210cm2.
(a) 4.2cm
(b) 7.5cm
(c) 5cm
(d) 8cm
Answer
Answer: (a) 4.2cm
Explanation:
CSA of cuboid = 2 (l h + b h)
210 = 2 (10 × h + 15 × h) = 2 (25h) = 50h
h = 210/50 = 4.2cm
16. Find the ratio of slant heights of cone, where the volume of cones of same height are in a ratio of 3:1.
(a) 1: 3
(b) 9: 1
(c) 1: √3
(d) √3 :1
Answer
Answer: (c) 1: √3
Explanation:
Vol of C1:Vol of C2 = 3:1
1/3 π r12 h1 : 1/3 π r22 h1 = 3:1
r12 h1: r22 h2 = 3:1
(r1: r2 )2 = 3:1 ( h1 = h2)
r1: r2 = √3: 1
Area of C1 = Area of C2
π r1 l1 = π r2 l2
l1: l2 = r2: r1 = 1: √3
Surface Area and Volume Class 9 MCQ
17. Find the area of cube if perimeter is 12x.
(a) x2
(b) 6x2
(c) 8x2
(d) x3
Answer
Answer: (a) x2
Explanation:
Perimeter = 12a = 12x
a = x = Side of cube
Area of cube = a2 = (x)2 = x2
18. The ratio of radii and slant heights of two cones are 1:1 and 2:3 respectively, find the ratio of their curved surface areas.
(a) 2:3
(b) 1:3
(c) 3:2
(d) 3:1
Answer
Answer: (a) 2:3
Explanation: S1 / S2 = πr1l1 / πr2l2
=( r1/r2) (l1/l2) = ( 1/1) ×(2/3) = 2/3
19. Find the volume of given figure
(a) 1550 cm2
(b) 1500 cm2
(c) 1437.3cm2
(d) 1410.7cm2
Answer
Answer: (c) 1437.3cm2
Explanation:
Shape is spherical shell
Volume = (4/3) π r3
= (4/3) × (22/7) × 73
= (4/3) × (22/7) × 7 × 49 = 1437.3 cm2
20. A room measuring 21m × 15m × 7m. Find the area to be painted, if the cost of painting is Rs 10/m2.
(a) 8000
(b) 8190
(c) 9000
(d) 8500
Answer
Answer: (b) 8190
Explanation: Area to be painted = CSA of room + Area of ceiling
= 2 (l h + b h) + l× b
= 2 (21 × 7 + 15 × 7) + 21× 15
= 2 (147 + 105) + 315
= 2 × 252 + 315 = 504 + 315 = 819 m2
Cost of painting = 819 × 10 = Rs 8190
21. Find the volume of cylinder, if the curved surface area of cylinder is 800cm2 and height is 20cm.
(a) 25 cm3
(b) 35.4 cm3
(c) 2547.77 cm3
(d) 44.3 cm3
Answer
Answer: (c) 2547.77 cm3
Explanation:
CSA of cylinder = 2πrh
800 = 2 π × r × 20
r = 20 / π cm
Volume of cylinder = πr2h = π × (20/π) × (20/π) × 20 = 2547.77cm3
22. TSA of right circular cone
(a) πrl
(b) πr2 (r +h)
(c) πr (l + r)
(d) πr2h
Answer
Answer: (c) πr (l + r)
23. Find the diagonal of a cube with side 4cm.
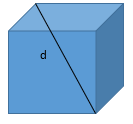
(a) 12cm
(b) 3√4 cm
(c) √3 cm
(d) 4√3 cm
Answer
Answer: (d) 4√3 cm
Explanation: d = √3 × side = 4√3 cm
24. Find the radius of sphere if volume is 1944π.
(a) 9(2)(1/3)
(b) 7.2
(c) 5√2
(d) 4
Answer
Answer: (a) 9(2)(1/3)
Explanation:
Vol of sphere = 4/3 πr3
1944π = 4/3 π × r3
r3 = 1944 × 3/4 = 1458
r = 9(2)(1/3)
25. Find the ratio of TSA and CSA of sphere.
(a) 1:2
(b) 1:3
(c) 1:4
(d) 1:1
Answer
Answer: (d) 1:1
Explanation:
TSA / CSA = 4 πr2 : 4 πr2 = 1: 1
Surface Area and Volume Class 9 MCQ
26. A ball is cut into two equal parts. Find the area of each part.
(a) 4πr2
(b) 2πr2
(c) 3πr2
(d) πr2
Answer
Answer: (b) 2πr2
Explanation:
A ball is a sphere. When we cut it into equal parts, we get two hemispheres of equal areas.
Area of hemisphere = 2πr2
27. If the radius of sphere is thrice. Find the new volume
(a) V2 = 2 V1
(b) V1 =V2 / 2
(c) V2 = 27 V1
(d) V2 = 9 V1
Answer
Answer: (c) V2 = 27 V1
Explanation:
Volume of new sphere = 4/3 πr3 = 4/3 π × (3r)3 =27 × 4/3 πr3
28. A gas cylinder of capacity 1000cm3 has 16kg of gas in it. If its height gets halved, find the amount of gas filled in it.
(a) 8kg
(b) 6kg
(c) 10kg
(d) 12kg
Answer
Answer: (a) 8kg
Explanation:
Volume of cylinder = πr2 h = πr2 × h1 = 1000
Vol of new cylinder = πr2 h2 = πr2 × h1/2 = 1000/2 = 500
In 1000cm3 capacity cylinder, 16kg gas can be filled
In 1cm3……………= 16/ 1000 kg
In 500cm3 …………= 16 × 500/ 1000 = 8kg gas
29. Find the CSA of cone when its radius is 5cm and slant height is 14cm.
(a) 22cm2
(b) 200cm2
(c) 220cm3
(d) 220cm2
Answer
Answer: (d) 220cm2
Explanation: CSA = π r l = 22/7 × 5 × 14 = 220cm2
MCQ Questions for Class 9 Maths
- Number Systems Class 9 MCQ with Answers
- Polynomials Class 9 MCQ with Answers
- Coordinate Geometry Class 9 MCQ Questions
- Linear Equations in Two Variables Class 9 MCQ with Answers
- Lines and Angles Class 9 MCQ with Answers
- Triangles Class 9 MCQ with Answers
- Quadrilaterals Class 9 MCQ Questions
- Circles Class 9 MCQ with Answers
- Constructions Class 9 MCQ
- Heron’s Formula Class 9 MCQ with Answers
- Surface Area and Volume Class 9 MCQ
- Statistics Class 9 MCQ
- Probability Class 9 MCQ with Answers
Frequently Asked Questions on Surface Area and Volume Class 9 MCQ
1. Are these MCQ on Surface Area and Volume Class 9 are based on 2021-22 CBSE Syllabus?
Yes . There are 29 MCQ’s on this Chapter in this blog.
2. Are you giving all the chapters of Maths Class 9 MCQs with Answers which are given in CBSE syllabus for 2021-22 ?
Yes, we are providing all the chapters of Maths Class 9 MCQs with Answers.