Square and Square Roots Class 8 Questions, deals with various types of questions which are as under:-
- Finding the perfect square
- Finding the number to be multiplied to make perfect square
- Finding the square of two-digit number
- Finding the value of expression using identity
- Finding the value of square root term
- Finding the value of unknown term using identity
- Word problems on Square root
Square and Square Roots Class 8 Questions – Finding the perfect square
Question 1:
Which one of the following is perfect square ?
488 , 732 , 121, 3482
Solution:
The numbers which end with 2 , 3, 7 or 8 cannot be the complete squares.
Since, 488 , 732 and 3482 end with 8 , 2, 2 , therefore, they cannot be perfect square.
But, 121 can be written as
121 = 11 x 11
Hence, 121 is a perfect square.
Square and Square Roots Class 8 Questions – Finding the number to be multiplied to make perfect square
Question 2:
What is the least number by which 450 should be multiplied, so that the product of the two numbers would be a perfect square?
Solution:
If we find the factors of 450 , we would get 450 = 3 x 3 x 5 x 5 x 2
If we draw out the factors in pairs, we would notice that we have pairs of 3 and 5 , but 2 is the only single number, which is not in pair.
Therefore if 450 is multiplied by 2 then the product would be a complete square.
Square and Square Roots Class 8 Questions – Finding the square of two digit number
Question 3:
What is the value of (91)²
Solution:
We know that (a-b)² = a² + b² + 2ab
When finding the square of a larger number, we can use this equation to break the larger number into parts, whose squares can be easily calculated
We can write 91 as ( 100 – 9 )
So
91² = (100-9)²
Applying (a-b)² = a² + b² + 2ab and substituting the value of a and b, we get
= 100² + 9² – 2 x 100 x 9
= 10000 + 81 – 1800
= 10081 – 1800
= 8281
Square and Square Roots Class 8 Questions – Finding the value of expression using identity
Question 4:
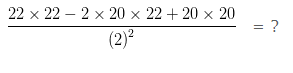
Solution:
We know that (a-b)² = a² + b² + 2ab
If we compare the above equation with the Numerator, we would find that the equation can be re-written as
= 22² – 2 x 20 x 22 + 20²
Or we can say that the given equation has value of
a = 22 and b = 20
So we can replace the numeration
22 x 22 – 2 x 20 x 22 + 20 x 20 with (22-20)² = 2²
Now putting these values in Numerator, we would get
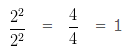
Question 5:
Find the value of 44² – 43² + 2²
Solution:
44² – 43² + 2²
We know that (a² – b²) = (a-b)(a+b)
a = 44 and b = 43
= ( 44 + 43 ) ( 44 – 43 ) + 4
= 87 x 1 + 4
= 87 + 4
= 91
Question 6:
The value of 555² – 554² ?
Solution:
We know that a² – b² = (a-b)(a+b)
If we compare the above equation to the problem , we find that
a = 555 and b = 554
So we can rewrite the above equation as
555² – 554² = ( 555 + 554 ) ( 555 – 554 )
= 1109 x 1
= 1109
Square and Square Roots Class 8 Questions – Finding the value of square root term
Question 7:

Solution:
In order to solve these type of problems, we first need to equate the value which has to be solved ![]() of the given equation in the given equation
of the given equation in the given equation
We can write √18 = 4.24
Replacing 18 by ( 2 x 9 ) in the given equation, and dividing both the sides by 9 , we would get
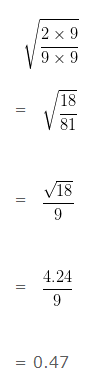
Square and Square Roots Class 8 Questions – Finding the value of unknown term using identity
Question 8:
If 42² – 40² = (12² – 10²) x Y, then the value of Y is ?
Solution:
Since,
a² – b² = (a-b) (a+b)
We can rewrite both the equation as
42² – 40² = (12² – 10²) x Y
( 42 + 40 ) x ( 42 – 40 ) = ( 12 + 10 ) x ( 12 – 10 ) x Y
82 x 2 = 22 x 2 x Y
164 = 44 x Y
Or,
Y = 164/44
Y = 41/11
Square and Square Roots Class 8 Questions – Word problems on Square root
Question 9:
In a conference hall of a school, 900 students were sitting in such a way that there were as many rows as there were students in a row. How many rows were there?
Solution:
Let the number of rows = Number of students in a row = x
Total number of students = Number of rows x Number of students in a row
Then
x × x = 900,
x² = 900
x=√900
= √ 3 x 3 x 5 x 5 x 2 x 2
= 3 x 5 x 2
= 30
Hence, the number of rows = Number of students in a row = 30
Question 10:
A group of People decided to collect as many paisa from each member of the group as is the number of members. If the total collection amounts to Rs. 11.56 , the number of members in the group is ?
Solution:
Funds collected in paisa= 11.56 x 100
= 1156
Funds collected= Numbers of the members of the group x Paisa collected from each memeber
Or
1156= Numbers of the members of the group x Paisa collected from each memeber
Let the Number of members of the group= x
Then Paisa collected from each member= x
Substituting these values in the given equation
1156= x × x,
x² = 1156
Or,
x = √1156
x = 34
Numbers of the members of the group = 34