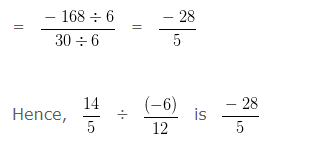Rational Numbers Class 7 Questions, deals with various concepts which are as under:-
- Additive Inverse of a Rational Number
- Equivalent Rational Numbers
- Addition of Rational Numbers
- Subtracting Rational Numbers
- Multiplication of Rational Numbers
- Dividing Rational Numbers
Rational Numbers Class 7 Questions – Equivalent Rational Numbers
- To obtain a rational number equivalent to the given rational number we have to multiply the numerator and denominator of a given rational number by the same nonzero number.
- To obtain a rational number equivalent to the given rational number we have to divide the numerator and denominator of a given rational number by a common divisor.
Example 1
Are 3/5 and 9/15 are equivalent Rational Numbers?
Explanation:
If two Rational Numbers are equivalent, the product obtained by Cross Multiplying them would also be equal
On Cross Multiplying the given Rational numbers
3/5 and 9/15
we get,
3 x 15 = 45
and 9 x 5 = 45
Since, 3 x 15 = 9 x 5
So, 3/5 = 9/15
Hence, 3/5 and 9/15 are equivalent Rational Number.
Equivalent Rational Number with given Numerator
Example 2
Express -8/6 as a Rational Number with Numerator 24.
Explanation:
Numerator of -8/6 = -8
We need to change the Numerator of -8/6 to 24
We need to find a number, with which we should multiply -8 so it is equal to 24
To obtain that number, we would need to divide 24 by -8 i.e,
24/(-8) = -3
So, we have to multiply both the Numerator and Denominator of given Rational Number by -3
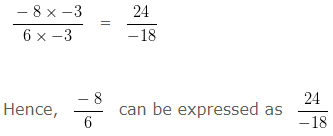
Equivalent Rational Number with given Denominator
Example 3
Express 16/25 as a Rational Number with Denominator -75.
Explanation:
Denominator of 16/25 = 25
We need to change the Denominator of 16/25 to -75
We need to find a number, with which we should multiply 25 so it is equal to -75
To obtain that number, we would need to divide -75 by 25 i.e,
(-75)/25 = -3
So, we have to multiply both the Numerator and Denominator of given Rational Number by -3
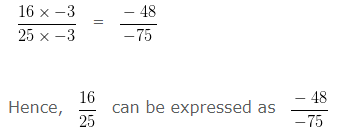
Rational Numbers Class 7 Questions – Additive Inverse of a Rational Number
Additive inverse of any rational number is that number with minus (negative) sign before it.
i.e, Additive inverse of a/b is -a/b
Example 4
Additive inverse of (-19)/10 is?
Explanation:
Additive inverse of any number is that number with minus (negative) sign before it.
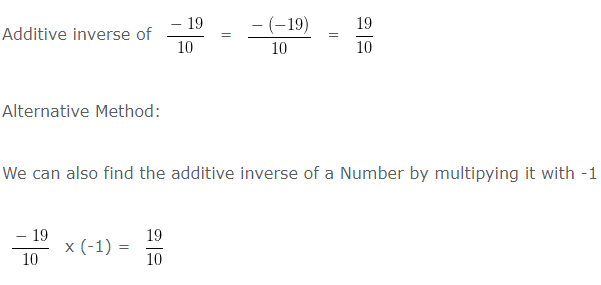
Addition of Rational Numbers
When we have to add two rational numbers, First we should convert each of them into a rational number with a positive denominator.
Addition of Rational Numbers When Denominator Are Equal
Question 5

Question 6
Find the sum of 19/13 and 11/(-13)
Explanation
To add two Rational Numbers, first their Denominators should be positive
So, we would first express 11/(-13) as a Rational Number with a positive Denominator.
Multiplying both the Numerator and Denominator by (-1)

Addition of Rational Numbers When Denominators Are Unequal
Question 7
Find the sum of 7/6 and 5/9?
Explanation
To add two Rational Numbers with different Denominator, we will first find the LCM of both the Denominators.
LCM of 6 and 9 is 18
Now we would divide such LCM by Denominator of first number and the result would be multiplied with both the numerator and denominator of such number
Dividing LCM by the Denominator of first number
18 ÷ 6 = 3
Multiplying both the Numerator and Denominator of 7/6 by the quotient i.e, 3
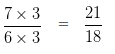
Dividing LCM by the Denominator of Second number
18 ÷ 9 = 2
Multiplying both the Numerator and Denominator of 5/9 by 2
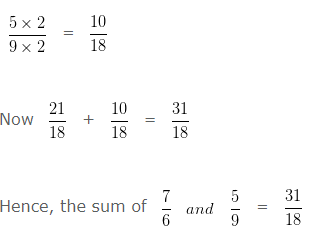
Question 8
Find the sum of 9/8 and 5/(-6)?
Explanation
To add two Rational Numbers,
first
their Denominators should be positive
So, we would first express 5/(-6) as a Rational Number with positive Denominator.
Multiplying both the Numerator and Denominator by (-1)
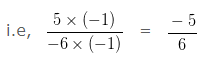
To add two Rational Numbers with different Denominator first we will find the LCM of both the Denominators.
LCM of 8 and 6 is 24
Divide LCM by the Denominator of first number
24 ÷ 8 = 3
We have to multiply , both the Numerator and Denominator of 9/8 by the quotient i.e, 3
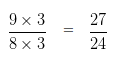
Divide LCM by the Denominator of second number
24 ÷ 6 = 4
We have to multiply , both the Numerator and Denominator of -5/6 by 4
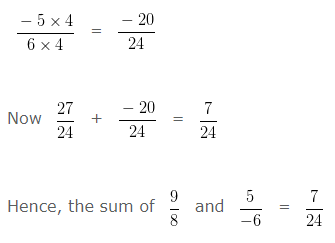
Rational Numbers Class 7 Questions – Subtracting Rational Numbers
Subtracting Rational Numbers When Denominators are Equal
Question 9
Subtract:
13/7 – 8/7
Explanation
Difference of Rational Numbers when Denominators are equal

Question 10
Subtract:
34/13 – 12/13
Explanation
Difference of Rational Numbers when Denominators are equal

Subtracting Rational Numbers When Denominators are Unequal
Question 11
Subtract:
3/4 – 2/7
Explanation
To subtract two Rational Numbers with different Denominators, first we will find the LCM of both the Denominators.
LCM of 4 and 7 is 28
Now we would divide such LCM by Denominator of first number and the result would be multiplied with both the numerator and denominator of such number
Divide LCM by the Denominator of first number
28 ÷ 4 = 7
We have to multiply , both the Numerator and Denominator of 3/4 by the quotient i.e, 7
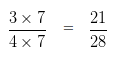
Divide LCM by the Denominator of second number
28 ÷ 7 = 4
We have to multiply , both the Numerator and Denominator of 2/7 by the quotient i.e, 4
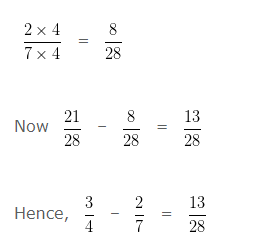
Question 12
Subtract:
5/4 – 3/5
Explanation
To subtract two Rational Numbers with different Denominators, first we will find the LCM of both the Denominators.
LCM of 4 and 5 is 20
Now we would divide such LCM by Denominator of first number and the result would be multiplied with both the numerator and denominator of such number
Divide LCM by the Denominator of first number
20 ÷ 4 = 5
We have to multiply , both the Numerator and Denominator of 5/4 by the quotient i.e, 5
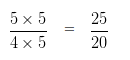
Divide LCM by the Denominator of second number
20 ÷ 5 = 4
We have to multiply , both the Numerator and Denominator of 3/5 by the quotient i.e, 4
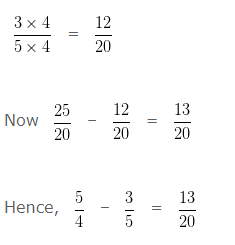
Rational Numbers Class 7 Questions – Multiplication of Rational Numbers
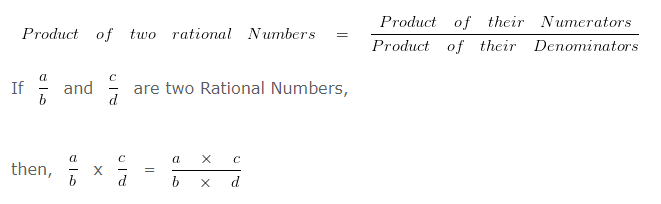
Question 13
Find the product of 15/7 and 3/5?
Explanation
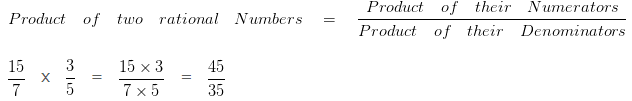
To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 45 and 35 is 5
Dividing both the Numerator and Denominator by their HCF
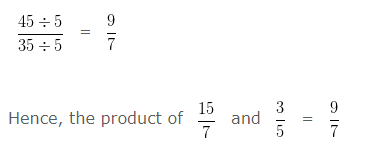
Question 14
Find the product of 9/7 and (-12)/8
Explanation

To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 108 and 56 is 4
Dividing both the Numerator and Denominator by their HCF
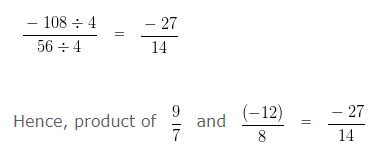
Question 15
Find the product of (-4)/7 and 8/12?
Explanation

To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 32 and 84 is 4
Dividing both the Numerator and Denominator by their HCF
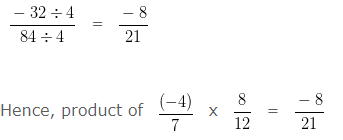
Question 16
Find the product of (-11)/8 x (-6)/5?
Explanation

To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 66 and 40 is 2
Dividing both the Numerator and Denominator by their HCF
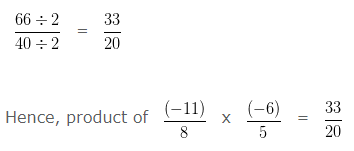
Rational Numbers Class 7 Questions – Dividing Rational Numbers
In order to divide a Rational Number by another Rational Number
We have to multiply first Rational Number with Reciprocal of the second Rational Number.
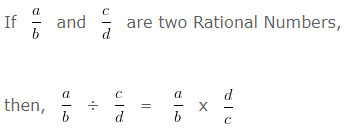
Question 17
Divide:
9/7 ÷ 3/4
Explanation
We have, 9/7 ÷ 3/4
In order to divide a Rational Number by another Rational Number
We have to multiply first Rational Number with Reciprocal of the second Rational Number.
We have 9/7 ÷ 3/4
(Reciprocal of 3/4 is 4/3 )
So we can say that,
9/7 ÷ 3/4
= 9/7 x 4/3
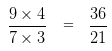
To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 36 and 21 is 3
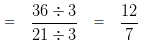
Question 18
Divide:
14/5 ÷ (-6)/12
Explanation
We have, 14/5 ÷ (-6)/12
In order to divide a Rational Number by another Rational Number
We have to multiply first Rational Number with Reciprocal of the second Rational Number
Since, Reciprocal of (-6)/12 is 12/(-6)
We can write the given equation as 14/5 ÷ (-6)/12
= 14/5 x 12/(-6)
To make the Denominator positive, we would multiply 12 and -6 by -1
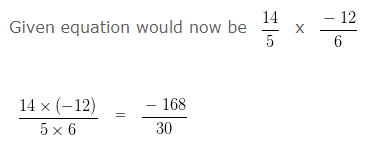
To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 168 and 30 is 6