NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2 – Quadrilaterals. This Exercise contains 7 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 9 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2 – Quadrilaterals
NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2 – Quadrilaterals
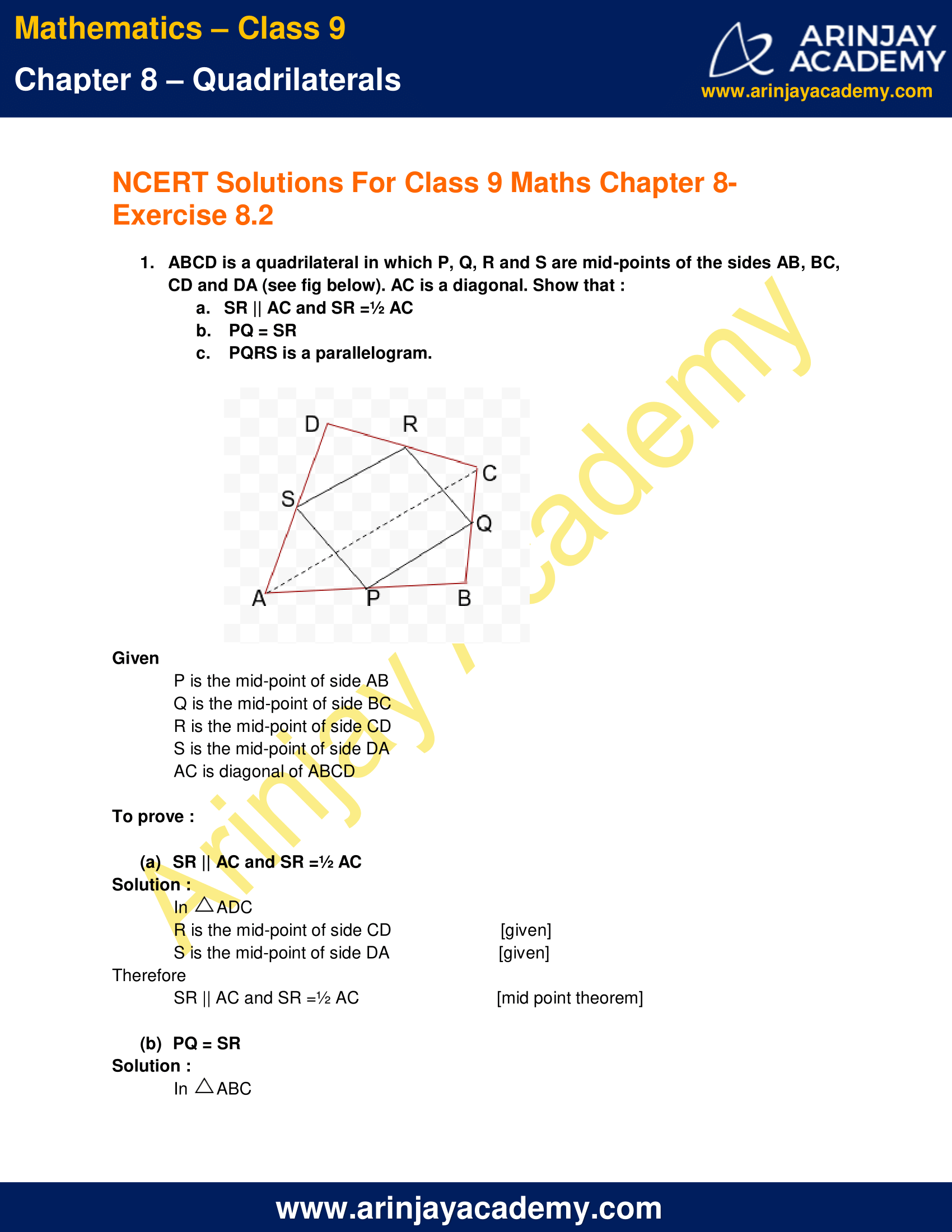
1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see fig below). AC is a diagonal. Show that :
a) SR || AC and SR =½ AC
b) PQ = SR
c) PQRS is a parallelogram.
                                                               Â
Given
P is the mid-point of side AB
Q is the mid-point of side BC
R is the mid-point of side CD
S is the mid-point of side DA|AC is diagonal of ABCD
 To prove :
(a) SR || AC and SR =½ AC
Solution :
In ΔADC
R is the mid-point of side CDÂ [given]
S is the mid-point of side DAÂ Â [given]
Therefore
SR || AC and SR =½ AC [mid point theorem]
(b) PQ = SR
Solution :
In ΔABC
P is the mid-point of side ABÂ [given]
Q is the mid-point of side BCÂ [given]
Therefore
PQ || AC and PQ =½ AC  [mid point theorem] (1)
Also
SR || AC and SR =½ AC  [from part (a)] (2)
From (1) and (2) we conclude that
SR ||PQ || ACÂ Â Â Â Â (3)
And , SR = PQ = ½ AC  (4)
Thus PQ = SRÂ Â Â [using (4)]
(c)Â Â PQRS is a parallelogram.
Solution:
In quadrilateral PQRS,
We have
PQ = SRÂ Â Â [from part (b)]
PQ || SRÂ Â Â [using (3)]
(A quadrilateral is a parallelogram if it’s opposite sides is equal and parallel.)
Therefore, PQRS is a parallelogram.
2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Given :
ABCD is a rhombus
P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively
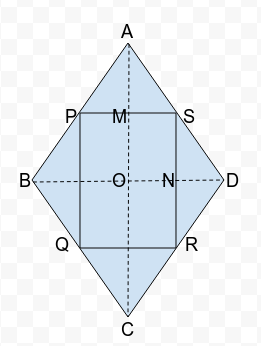
To prove :
Quadrilateral PQRS is a rectangle
Solution :
In ΔABD
P is the mid-point of side AB [given]
S is the mid-point of side AD [given]
Therefore
PS || BD and PS =½ BD [By mid point theorem] (1)
In ΔBCD
Q is the mid-point of side BCÂ [given]
R is the mid-point of side CDÂ Â [given]
Therefore
QR || BD and QR =½ BD  [mid point theorem] (2)
Similarly we can prove that
PQ || AC and PQ =½ AC   (3)
SR || AC and SR =½ AC   (4)
Therefore using (1), (2), (3) and (4) we conclude that PQRS is a parallelogram.
(A quadrilateral is a parallelogram if its opposite sides are equal & parallel)
In quadrilateral MONS
OM || SNÂ Â Â Â Â [ using (4) AC || QR]
SM || ONÂ Â Â Â Â [ using (1) PQ || BD]
∠MON = 900  [diagonals of a rhombus bisect perpendicularly]
We know that a quadrilateral having parallel opposite sides with one of its angles equal to 900 is a rectangle.
Therefore MONS is a rectangle
Hence, ∠PSN = 900
Thus, Parallelogram PQRS has one angle as right angle and so it is a rectangle.
So, we get PQRS is a rectangle.
3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Given :
Let ABCD be a rectangle in which P, Q, R, S are the mid-points of sides AB, BC, CD and DA respectively.
PQ, QR, RS and SP are joined such that a quadrilateral PQRS is formed.
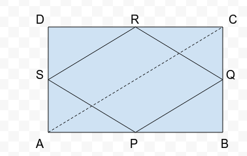
To Prove:
PQRS is a rhombus.
 Construction :
Divide the rectangle into two triangles by joining AC.
 Solution :
In ∆ABC, P and Q are the mid-points of the sides AB and BC.
Therefore, [By mid point theorem]
PQ || AC  & PQ =½ AC  … (a)
Similarly, in ∆ADC, [By mid point theorem]
SR || AC & SR =½ AC  … (b)
From (a) and (b), we get
PQ || SRÂ Â &Â PQ = SRÂ Â Â …(c)
In quadrilateral PQRS, opposite sides PQ and SR are parallel and equal.[From c)]
Therefore PQRS is a parallelogram.
Also
AS = BQÂ Â Â [Halves of equal sides are also equal.]Â … (d)
In ∆APS and ∆BPQ
AP = BPÂ Â Â Â [P is the mid-point of AB]
AS = BQÂ Â Â Â Â [from (d)]
∠PAS = ∠PBQ  [Each angle is 90° as ABCD is a rectangle.]
∆APS ≅ ∆BPQ  [SAS criteria of congruence]
PS = PQÂ Â Â …(e)
We know that if the adjacent sides of a parallelogram are equal then it is a Rhombus.
From (c) and (e), we conclude that PQRS is a rhombus.
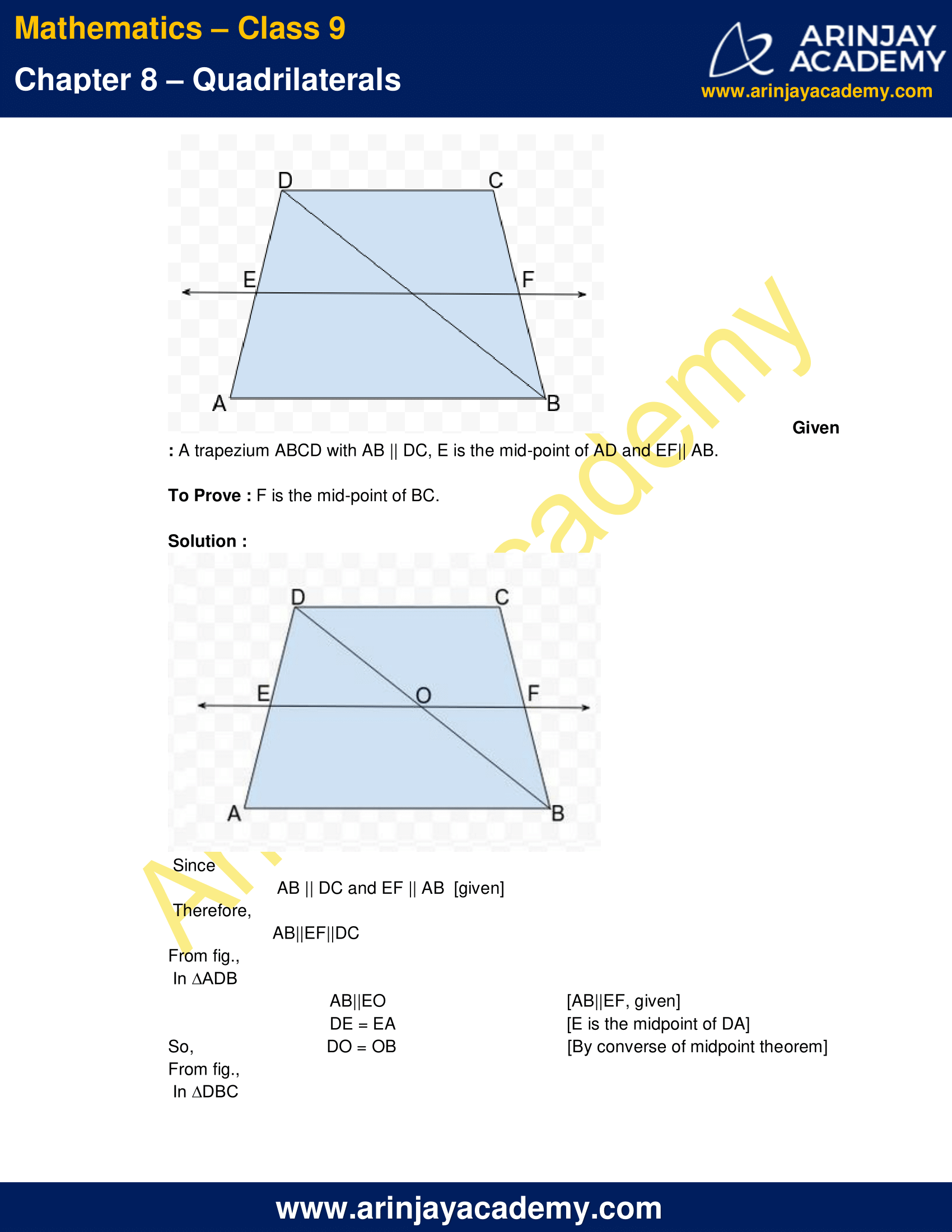
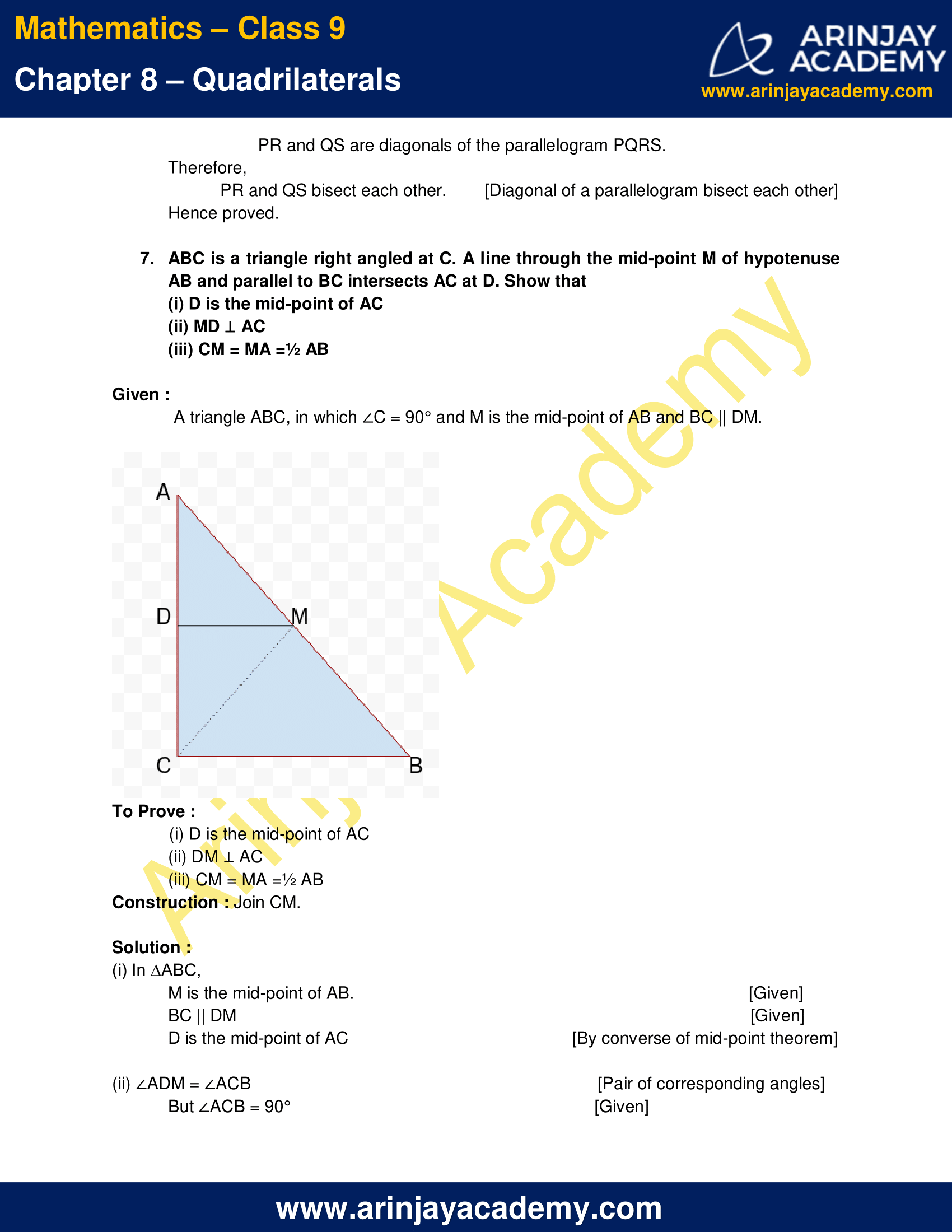
 4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see fig. below). Show that F is the mid-point of BC.
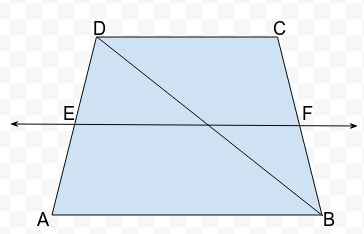
Given : A trapezium ABCD with AB || DC, E is the mid-point of AD and EF|| AB.
To Prove : F is the mid-point of BC.
Solution :
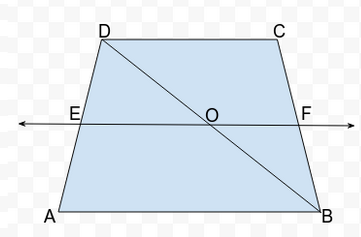
Since,
AB || DC and EF || ABÂ [given]
Therefore,
AB||EF||DC
From fig.,
In ∆ADB
AB||EOÂ Â Â [AB||EF, given]
DE = EAÂ Â Â [E is the midpoint of DA]
So, DO = OBÂ [By converse of midpoint theorem]
From fig.,
In ∆DBC
DC||OFÂ Â Â Â [DC||EF, given]
DO = OBÂ Â Â [proved above]
Therefore,
CF = FBÂ Â Â Â [By converse of midpoint theorem]
Thus, we conclude that F is the mid-point of BC.
Hence proved.
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see fig. below). Show that the line segments AF and EC trisect the diagonal BD.
                              Â
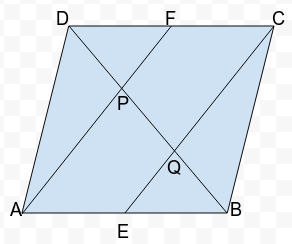
Given : A parallelogram ABCD, in which E and F are mid-points of sides AB and DC respectively.
So, AE =½ AB
CF =½ DC
To Prove : DP = PQ = QB=1/3 BD
Solution :
We have
AE =½ AB  [given]
CF =½ DC  [given]
Also
AB = DC and AB || DC [opposite sides of a parallelogram are equal & parallel]
Therefore,
AE = CF and AE || CF
Hence the quadrilateral AECF is a parallelogram as one pair of opposite sides is parallel and equal.
In ∆BAP,
E is the mid-point of ABÂ [given]
EQ || APÂ Â Â [AECF is a parallelogram]
Therefore,
Q is mid-point of PB [By converse of mid-point theorem]
Or, PQ = QBÂ Â Â (1)
Similarly,
In ∆DQC,
P is the mid-point of DQÂ Â Â Â Â [By converse of midpoint theorem]
Or, DP = PQ   (2)
Using (1) and (2), we have
DP = PQ = QB=1/3 BD
Or, line segments AF and EC trisect the diagonal BD.
6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Given : ABCD is a quadrilateral in which PR and QS are the line segments joining the mid-points of opposite sides.
                                         Â
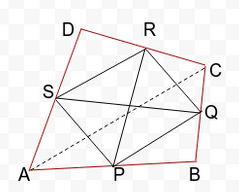
To Prove : PR and QS bisect each other.
Construction : Join PQ, QR, RS, SP and AC.
Solution :
In ∆ABC, P and Q are mid-points of AB and BC respectively.
PQ =½ AC and PQ || AC   (1) [By midpoint theorem]
In ∆ADC, S and R are mid-points of AD and CD respectively.
SR =½ AC and SR || AC   (2) [By midpoint theorem]
From (1) and (2), we get
PQ = SR and PQ || SR
We know that a quadrilateral is a parallelogram if it’s one pair of opposite sides is equal and parallel.
Therefore, PQRS is a parallelogram.
Now, PR and QS are diagonals of the parallelogram PQRS.
Therefore, PR and QS bisect each other. [Diagonal of a parallelogram bisect each other]
Hence proved.
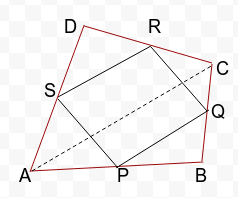
7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA =½ AB
 Given :
A triangle ABC, in which ∠C = 90° and M is the mid-point of AB and BC || DM.
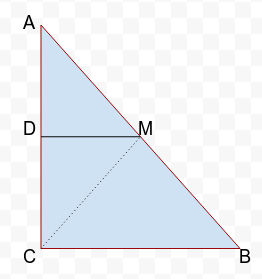
To Prove :
(i) D is the mid-point of AC
(ii) DM ⊥ AC
(iii) CM = MA =½ AB
Construction : Join CM.Â
Solution :
(i) In ∆ABC,
M is the mid-point of AB. [Given]
BC || DMÂ Â [Given]
D is the mid-point of ACÂ [By converse of mid-point theorem]
(ii) ∠ADM = ∠ACB  [Pair of corresponding angles]
But ∠ACB = 90°  [Given]
So,  ∠ADM = 90°
Also,
∠ADM + ∠CDM = 180°  [Linear pair]
Therefore, ∠CDM = 90°
Hence, MD ⊥ AC
Proved.
(iii) AD = DC     (1)[ ∵ D is the mid-point of AC part(i)]
In ∆ADM and ∆CMD, we have
∠ADM = ∠CDM  [Each angle is 90°]
AD = DCÂ Â Â Â [From part (i)]
DM = DMÂ Â Â [Common]
∆ADM ≅ ∆CDM   [SAS criteria of congruence]
Thus,
CM = MAÂ Â Â Â Â Â (2)Â [By C.P.C.T.]
Since M is mid-point of AB(given),
MA =½ AB    (3)
So, CM = MA =½ AB [From (2) and (3)]
Hence Proved.
NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2 – Quadrilaterals, has been designed by the NCERT to test the knowledge of the student on the following topics:-
- The Mid-point Theorem
– The line segment joining the mid-points of two sides of a triangle is parallel to the third side
– The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.1 – Areas of Parallelograms And Triangles can be accessed by clicking here.
NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.2 – Quadrilaterals
