Download NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1 – Triangles. This Exercise contains 8 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 7 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1 – Triangles





NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1 – Triangles
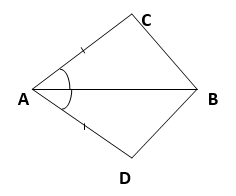
1. In quadrilateral ACBD,
AC = AD and AB bisects ∠ A (see Figure).
Show that ∆ ABC ≅ ∆ ABD. What can you say about BC and BD?
Solution :
In ∆ABC and ∆ABD,
AC = AD (∵ Given)
∠CAB = ∠DAB (∵ AB bisects ∠A)
AB = AB (∵ Common)
=> ∆ABC ≅ ∆ABD (By SAS congruence rule)
=> BC = BD (By CPCT)
=> BC and BD are of equal lengths.
Hence Proved.
2. ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA (see Figure).
Prove that
(i) ∆ ABD ≅ ∆ BAC
(ii) BD = AC
(iii) ∠ ABD = ∠ BAC.
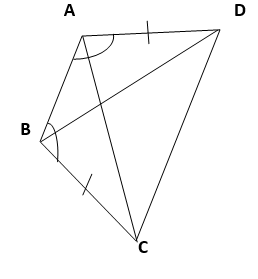
Solution :
In ∆ABD and ∆BAC,
AD = BC (∵ Given)
∠DAB = ∠CBA (∵ Given)
AB = BA (∵ Common)
=> ∆ABD ≅ ∆BAC (By SAS congruence rule)
=> BD = AC (By CPCT)
And, ∠ABD = ∠BAC (By CPCT)
Hence Proved.
3. AD and BC are equal perpendiculars to a line segment AB (see Figure). Show that CD bisects AB.
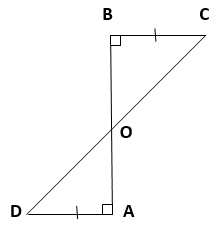
Solution :
In ∆BOC and ∆AOD,
∠BOC = ∠AOD (∵ Vertically opposite angles)
∠CBO = ∠DAO (∵ Each 90º)
BC = AD (∵ Given)
=> ∆BOC ≅ ∆AOD (AAS congruence rule)
=> BO = AO (By CPCT)
=> CD bisects AB.
Hence Proved.
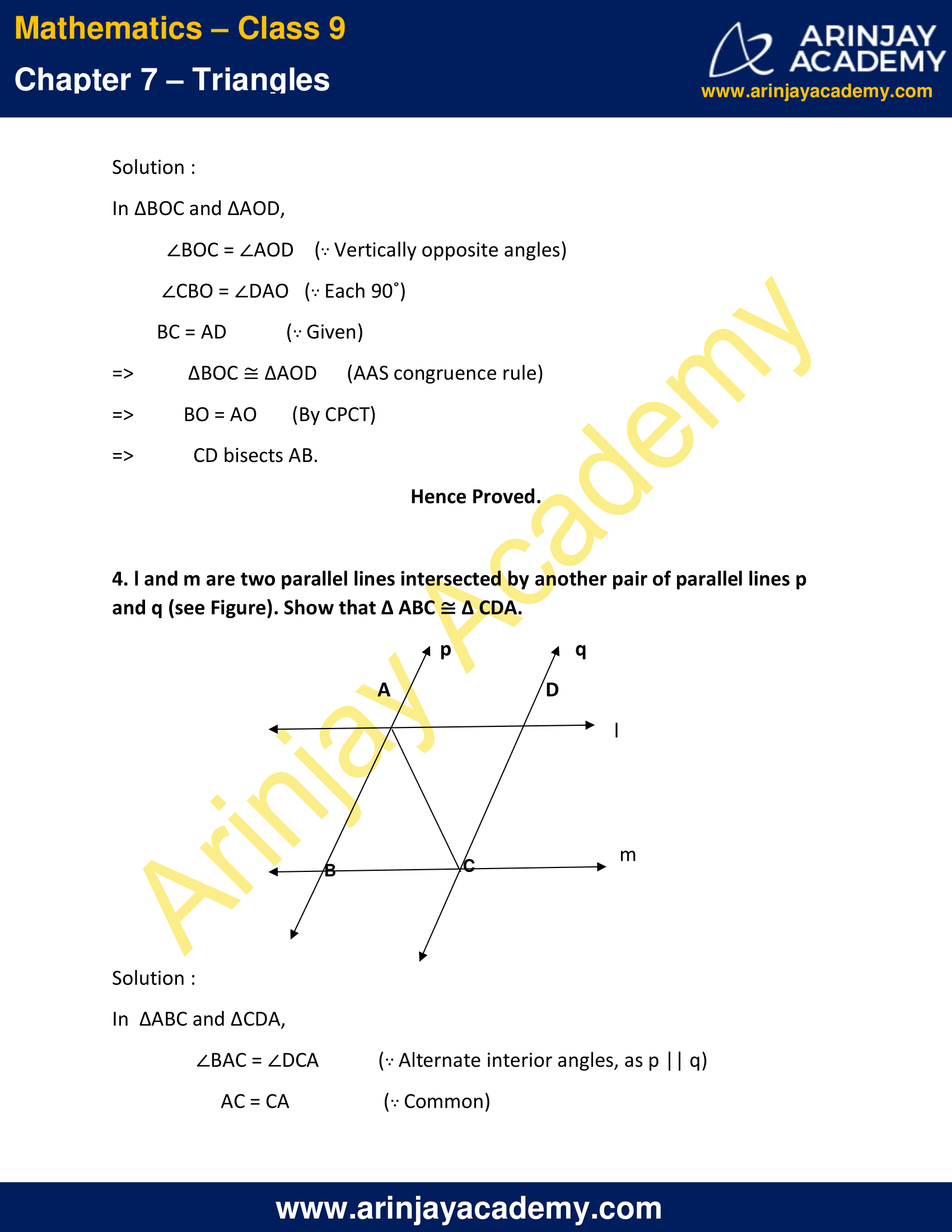
4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Figure). Show that ∆ ABC ≅ ∆ CDA.
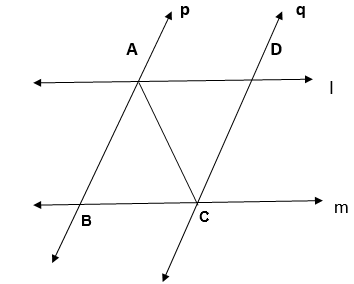
Solution :
In ∆ABC and ∆CDA,
∠BAC = ∠DCA (∵ Alternate interior angles, as p || q)
AC = CA (∵ Common)
∠BCA = ∠DAC (∵ Alternate interior angles, as l || m)
=> ∆ABC ≅ ∆CDA (By ASA congruence rule)
5. Line l is the bisector of an angle ∠ A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠ A (see Figure).
Show that:
(i) ∆ APB ≅ ∆ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.
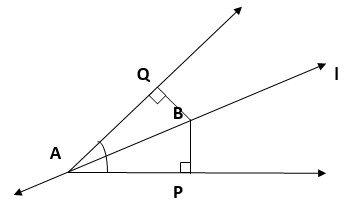
Solution :
In ∆APB and ∆AQB,
∠APB = ∠AQB (∵ Each 90º)
∠PAB = ∠QAB (∵ l is the angle bisector of ∠A)
AB = AB (∵ Common)
=> ∆APB ≅ ∆AQB (By AAS congruence rule)
=> BP = BQ (By CPCT)
It can be said that B is equidistant from the arms of ∠A.
6. In given Figure, AC = AE, AB = AD and ∠ BAD = ∠ EAC. Show that BC = DE.
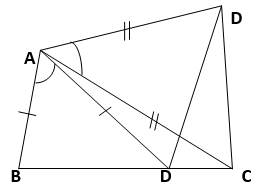
Solution :
Given,
∠BAD = ∠EAC
∠BAD + ∠DAC = ∠EAC + ∠DAC
∠BAC = ∠DAE
In ∆BAC and ∆DAE,
AB = AD (∵ Given)
∠BAC = ∠DAE (∵ Proved above)
AC = AE (∵ Given)
=> ∆BAC ≅ ∆DAE (∵ By SAS congruence rule)
=> BC = DE (∵ By CPCT)
Hence Proved
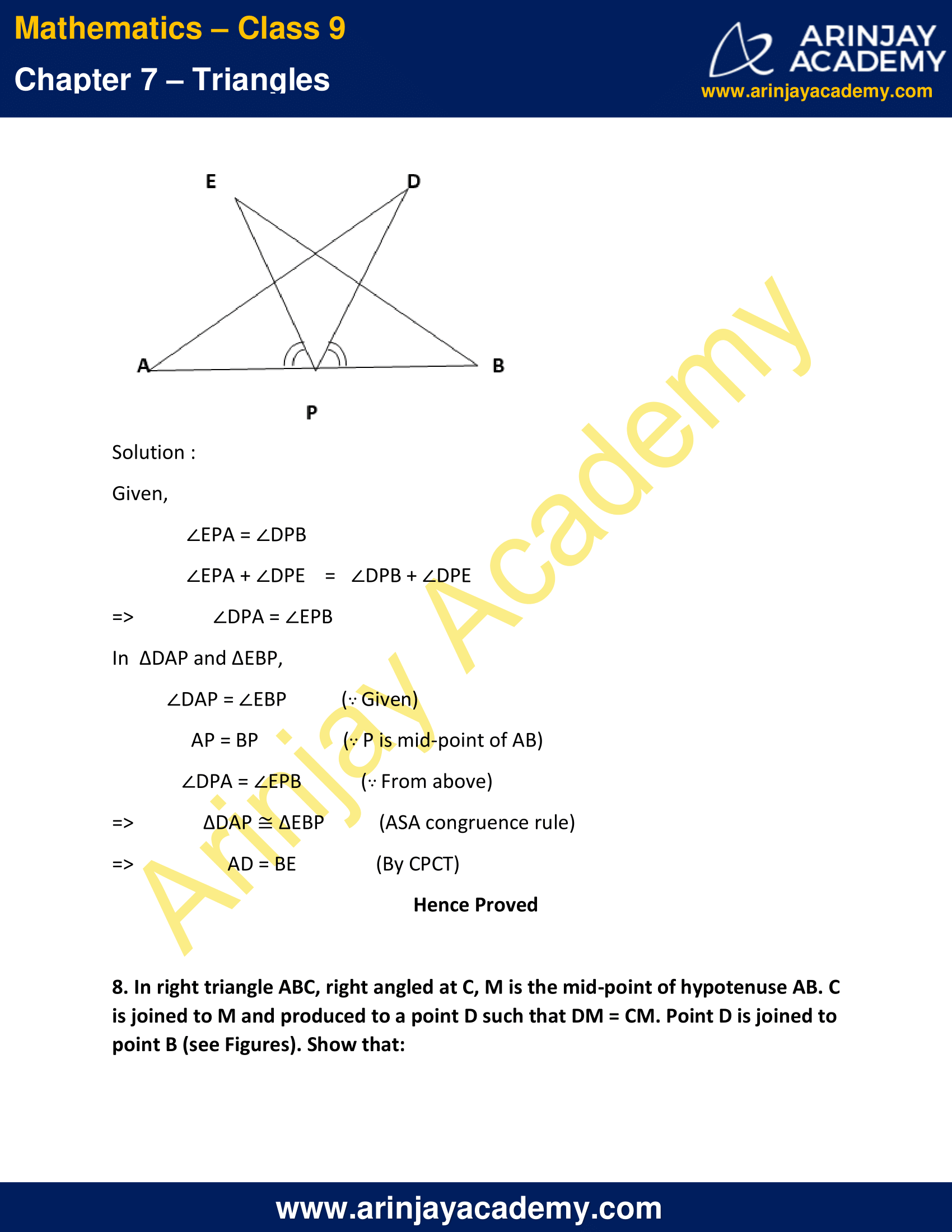
7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB (see Figure).
Show that
(i) ∆ DAP ≅ ∆ EBP
(ii) AD = BE
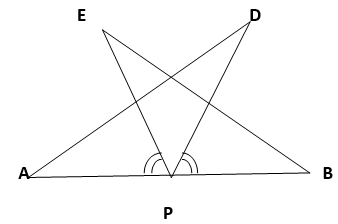
Solution :
Given,
∠EPA = ∠DPB
∠EPA + ∠DPE = ∠DPB + ∠DPE
=> ∠DPA = ∠EPB
In ∆DAP and ∆EBP,
∠DAP = ∠EBP (∵ Given)
AP = BP (∵ P is mid-point of AB)
∠DPA = ∠EPB (∵ From above)
=> ∆DAP ≅ ∆EBP (ASA congruence rule)
=> AD = BE (By CPCT)
Hence Proved
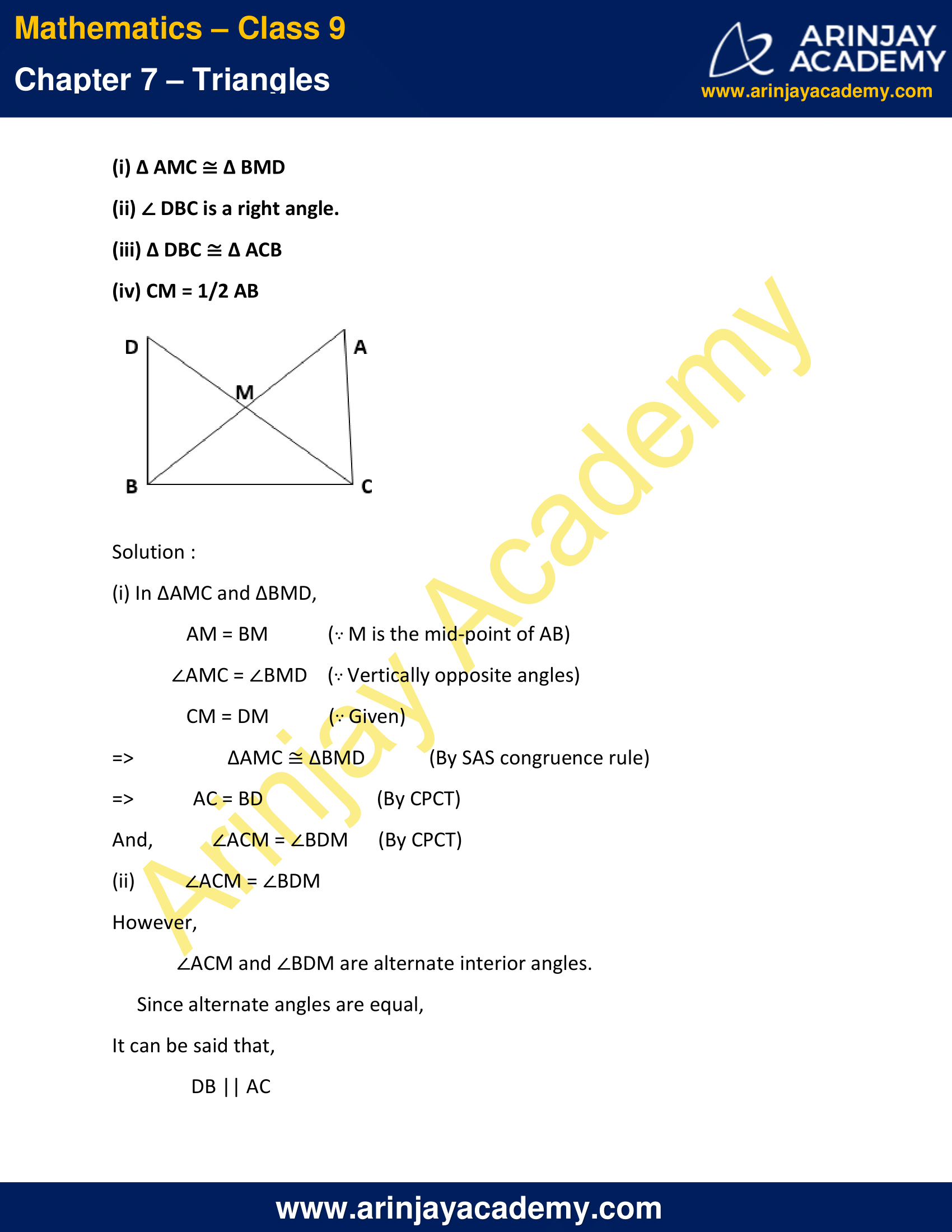
8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Figures). Show that:
(i) ∆ AMC ≅ ∆ BMD
(ii) ∠ DBC is a right angle.
(iii) ∆ DBC ≅ ∆ ACB
(iv) CM = 1/2 AB
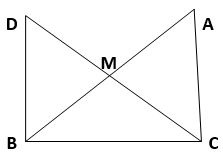
Solution :
(i) In ∆AMC and ∆BMD,
AM = BM (∵ M is the mid-point of AB)
∠AMC = ∠BMD (∵ Vertically opposite angles)
CM = DM (∵ Given)
=> ∆AMC ≅ ∆BMD (By SAS congruence rule)
=> AC = BD (By CPCT)
And, ∠ACM = ∠BDM (By CPCT)
(ii) ∠ACM = ∠BDM
However,
∠ACM and ∠BDM are alternate interior angles.
Since alternate angles are equal,
It can be said that,
DB || AC
∠DBC + ∠ACB = 180º (∵ Co-interior angles)
∠DBC + 90º = 180º
=> ∠DBC = 90º
(iii) In ∆DBC and ∆ACB,
DB = AC (∵ Already proved)
∠DBC = ∠ACB (∵ Each 90 )
BC = CB (∵ Common)
=> ∆DBC ≅ ∆ACB (SAS congruence rule)
(iv) ∆DBC ≅ ∆ACB
AB = DC (By CPCT)
AB = 2 CM
=> CM = (1/2) AB
Hence Proved.
NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1 – Triangles, has been designed by the NCERT to test the knowledge of the student on the following topics:-
- Congruence of Triangles
- Criteria for Congruence of Triangles
– SAS congruence rule
– ASA congruence rule
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.2 – Triangles can be accessed by clicking here.
Download NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1 – Triangles
