Download NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.3 – Lines and Angles. This Exercise contains 6 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 7 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.3 Lines and Angles





NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.3 Lines and Angles
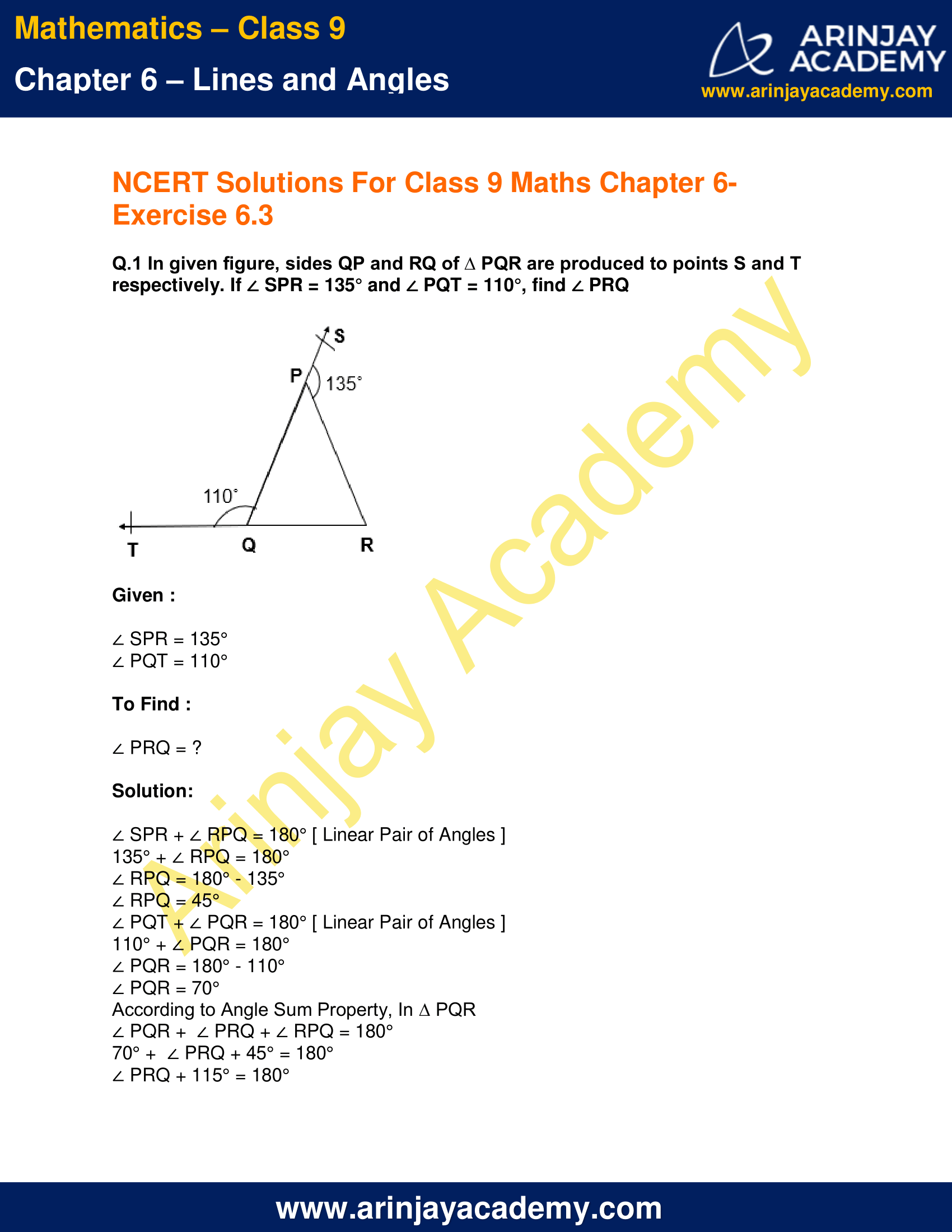
Q.1 In given figure, sides QP and RQ of ∆ PQR are produced to points S and T respectively. If ∠ SPR = 135° and ∠ PQT = 110°, find ∠ PRQ
Given :
∠ SPR = 135°
∠ PQT = 110°
To Find :
∠ PRQ = ?
Solution:
∠ SPR + ∠ RPQ = 180° [ Linear Pair of Angles ]
135° + ∠ RPQ = 180°
∠ RPQ = 180° – 135°
∠ RPQ = 45°
∠ PQT + ∠ PQR = 180° [ Linear Pair of Angles ]
110° + ∠ PQR = 180°
∠ PQR = 180° – 110°
∠ PQR = 70°
According to Angle Sum Property, In ∆ PQR
∠ PQR + ∠ PRQ + ∠ RPQ = 180°
70° + ∠ PRQ + 45° = 180°
∠ PRQ + 115° = 180°
∠ PRQ = 180° – 115°
∠ PRQ = 65°
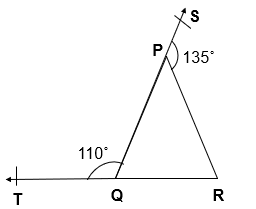
Q. 2 In given figure, ∠ X = 62°, ∠ XYZ = 54°. If YO and ZO are the bisectors of ∠ XYZ and ∠ XZY respectively of ∆ XYZ, find ∠ OZY and ∠ YOZ
Given :
∠ X = 62°
∠ XYZ = 54°
YO and ZO are bisectors of ∠ XYZ & ∠ XZY
To Find :
∠ OZY = ?
∠ YOZ = ?
Solution:
According to Angle Sum Property, In ∆ XYZ
∠ XYZ + ∠ YZX + ∠ ZXY = 180°
54° + ∠ YZX + 62° = 180°
∠ YZX + 116° = 180°
∠ YZX = 180° – 116°
∠ YZX = 64°
∠ OZY = 64°/2
∠ OZY = 32° [ OZ is angle bisector of ∠ YZX ]
∠ OYZ = 54°/2 = 27° [ OY is angle bisector of ∠ XYZ ]
According to Angle Sum Property, In ∆ OYZ
∠ OYZ + ∠ OZY + ∠ YOZ = 180°
27° + 32° + ∠ YOZ = 180°
59° + ∠ YOZ = 180°
∠ YOZ = 180° – 59°
∠ YOZ = 21°
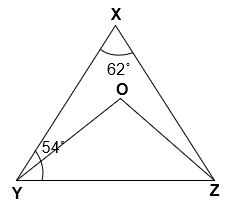
Q.3 In given figure, if AB || DE, ∠ BAC = 35° and ∠ CDE = 53°, find ∠ DCE.
Given :
AB || DE
∠ BAC = 35°
∠ CDE = 53°
To Find :
∠ DCE = ?
Solution:
∠ BAC = ∠ CED = 35° [ Alternate interior angles ]
According to Angle Sum Property, In ∆ CDE
∠ CDE + ∠ CED + ∠ DCE = 180°
53° + 35° + ∠ DCE = 180°
88° + ∠ DCE = 180°
∠ DCE = 180° – 88°
∠ DCE = 92°
Q. 4 In given figure, if lines PQ and RS intersect at point T, such that ∠ PRT = 40°, ∠ RPT = 95° and ∠ TSQ = 75°, find ∠ SQT.
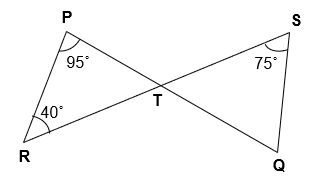
Given :
∠ PRT = 40°
∠ RPT = 95°
∠ TSQ = 75°
To Find : ∠ SQT = ?
Solution:
According to Angle Sum Property, In ∆ PRT
∠ RPT + ∠ PRT + ∠ PTR = 180°
95° + 40° + ∠ PTR = 180°
135° + ∠ PTR = 180°
∠ PTR = 180° – 135°
∠ PTR = 45°
∠ PTR = ∠ STQ = 45° [ Alternate interior angle ]
According to Angle Sum Property, In ∆ STQ
∠ QST + ∠ STQ + ∠ SQT = 180°
75° + 45° + ∠ SQT = 180°
120° + ∠ SQT = 180°
∠ SQT = 180° – 120°
∠ SQT = 60°
Q.5 In given figure, if PQ ⊥ PS, PQ || SR, ∠ SQR = 28° and ∠ QRT = 65°, then find the values of x and y.
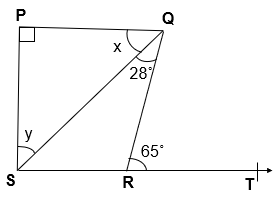
Given :
PQ ⊥ PS
PQ || SR
∠ SQR = 28°
∠ QRT = 65°
To Find :
x = ?
y = ?
Solution:
∠ PQR = ∠QRT [ Alternate interior angle ]
x + 28° = 65°
x = 65° – 28°
x = 37°
According to Angle Sum Property, In ∆PQS
x + y + ∠ QPS = 180°
37° + y + 90° = 180°
y + 127° = 180°
y = 180° – 127° = 53°
Q.6 In given figure, the side QR of ∆ PQR is produced to a point S. If the bisectors of ∠ PQR and ∠ PRS meet at point T, then prove that ∠ QTR = 1/2 ∠ QPR
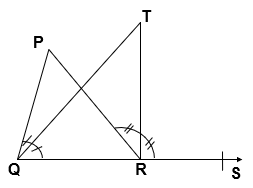
Solution:
In ∆ QTR, ∠ TRS is an Exterior Angle.
∠ QTR + ∠ TQR = ∠ TRS
∠ QTR = ∠ TRS – ∠ TQR ——– 1
In ∆ PQR, ∠ PRS is an Exterior Angle.
∠ QPR + ∠ PQR = ∠ PRS
∠ QPR + 2 ∠ TQR = 2 ∠ TRS
∠ QPR = 2 ( ∠ TRS – ∠ TQR )
Using Eq 1, ∠ QPR = 2 QTR
∠ QTR = 1/2 ∠ QPR
NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.3 – Lines and Angles, has been designed by the NCERT to test the knowledge of the student on the topic – Angle Sum Property of a Triangle
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1 – Triangles can be accessed by clicking here.
Download NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.3 – Lines and Angles
