Download NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.1 – Heron’s Formula. This Exercise contains 6 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for other Chapters, you can click the link at the end of this Note.
NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.1 – Heron’s Formula




NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.1 – Heron’s Formula
1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Solution :
Given,
Perimeter of the equilateral triangle = 180 cm
Side of the equilateral triangle = a cm
We know that,
Perimeter of the equilateral triangle is = 3a
=> 3a = 180 cm
=> a = 60 cm
=> semi-perimeter
s = (3a/2) = 90 cm
Area of the triangle
= √s(s-a)(s-b)(s-c) [ Here a = b = c = 60 cm ]
= √(90)(90-60)(90-60)(90-60)
= √(90)(30)(30)(30)
= √(30^4) x 3
= (30)2√3 cm2
= 900√3 cm2
Area of the signal board = 900√3 cm2
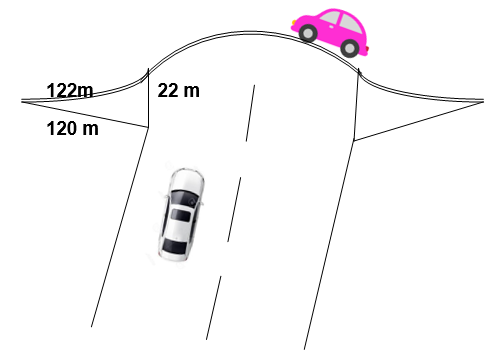
2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Figure). The advertisements yield an earning of Rs. 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
Solution :
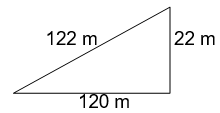
Lengths of the sides of the triangle are 122 m, 120 m, 22 m.
Semi-perimeter s = (122+120+22/2)
= 132 m
Area of the triangle
= √s(s-a)(s-b)(s-c)
= √(132)(132-120)(132-122)(132-22)
= √ (132)(12)(10)(110)
= √ (12)(11)(12)(10)(11)(10)
= √12 x 11 x 10
= √1320 m2
Rent of 1 m2 per year = Rs. 5000
=> Rent of 1 m2 per month = Rs. (5000/12)
=> Rent of 1 m2 for 3 months = Rs. (5000/12) x3
=> Rent of 1 m2 for 3 months = Rs. 1250
=> Rent of 1320 m2 for 3 months = Rs. 1250 x 1320
= Rs. 1650000
=> The company had paid = Rs. 1650000
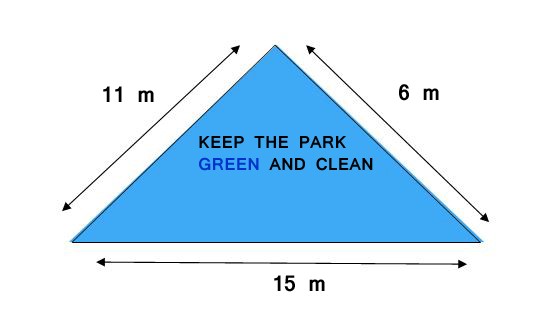
3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Figure). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.
Solution :
Area painted in colour = Area of the triangle
Area of the triangle :
= √s(s-a)(s-b)(s-c)
s = (11+6+15/2) = 16 m
a = 11 m
b = 6 m
c = 15 m
Area of the trianlge = √(16)(16-11)(16-6)(16-15)
= √(16)(5)(10)(1)
= √800 m2 = 20√2 m
Area painted in colour = 20√2 m.
4. Find the area of a triangle two sides of which are 18cm and 10cm and the perimeter is 42cm.
Solution :
Perimeter = Sum of the lengths of sides of the triangle.
=> 42 = 18 + 10 + x
=> x = 42 – 28
=> x = 14 cm
Lengths of the triangle : 18 cm, 10 cm, 14 cm.
Semi-perimeter, s = (18+10+14/2)
s = 21 cm
Area of the triangle = √s(s-a)(s-b)(s-c)
= √(21)(21-18)(21-10)(21-14)
= √(21)(3)(11)(7)
= 21√11 m2
5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.
Solution :
Given the ratio of lengths of the sides = 12 : 17 : 25
Let the proportionate value = x
=> Lengths of the sides of the triangle = 12x cm, 17x cm, 25x cm
Perimeter = Sum of the lengths of the triangles
=> 540 = 12x + 17x + 25x
=> 540 = 54x
=> x = 10 cm
=> Lengths of the sides of the triangle = 120 cm, 170 cm, 250 cm
Semi-perimeter,
s = (120 + 170 + 250)/2
s = 270 cm
Area of the triangle = √s(s-a)(s-b)(s-c)
= √(270)(270-120)(270-170)(270-250)
= √(270)(150)(100)(20)
= 9000 cm2
6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution :
Let, the lengths of the sides of the triangle are a, b, c.
Let the equal sides are a and b.
=> a = 12 cm b = 12 cm
Since the perimeter of the triangle is 30 cm,
=> a + b + c = 30 cm
=> 12 + 12 + c = 30 cm
=> c = 6 cm
Semi-perimeter s = (12+12+6/2)
s = 15 cm
Area of the triangle = √s(s-a)(s-b)(s-c)
= √(15)(15-12)(15-12)(15-6)
= √(15)(3)(3)(9)
= 9√15 cm2
NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.1 – Heron’s Formula, has been designed by the NCERT to test the knowledge of the student on the topic – Area of a Triangle — by Heron’s Formula
Download NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.1 – Heron’s Formula
