NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.2 – Understanding Quadrilaterals, has been designed by the NCERT to test the knowledge of the student on the topic – Sum of the Measures of the Exterior Angles of a Polygon
NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.2



NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.2
1. Find x in the following figures.
a)
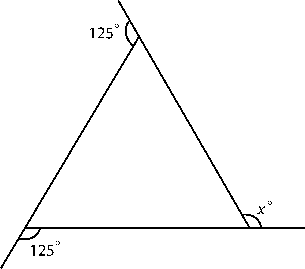
Solution:
Sum of exterior angles = 360°
125° + 125° + x = 360°
250° + x = 360°
x = 360° – 250°
x = 110°
b)
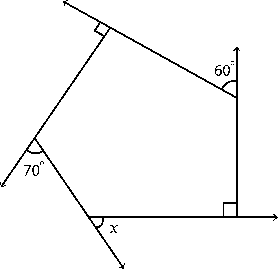
Solution:
Sum of exterior angles = 360°
90° + 70° + x + 90° + 60° = 360°
310° + x = 360°
x = 360° – 310°
x = 50°
Find the measure of each exterior angle of a regular polygon of
i) 9 sides
Solution:
Total exterior angles = 9
Sum of exterior angles = 360°
Each exterior angle = (360°/9) = 40°
ii) 15 sides
Solution:
Total exterior angles = 15
Sum of exterior angles = 360°
Each exterior angle = (360°/15) = 24°
3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Solution:
Sum of exterior angles = 360°
Each exterior angle = 24°
Total number of exterior angles = (360°/24°) = 15
Therefore, the polygon has 15 sides.
7. How many sides does a regular polygon have if each of its interior angle is 165°?
Solution:
Each interior angle = 165°
Interior angle + exterior angle = 180°
165° + exterior angle = 180°
Exterior angle = 15°
Sum of exterior angles = 360°
Total number of exterior angles = (360°/15°) = 24
Therefore, the polygon has 24 sides.
5. (a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Solution:
(a) Number of sides of a polygon with 22° as exterior angle = (360°/22°) = (180/11)
The number of sides cannot be a fraction
∴ A regular polygon cannot have each exterior angle as 22°
(b) Exterior angle = 180° – interior angle
Exterior angle = 180° – 22° = 158°
Number of sides of a polygon with 158° as exterior angle = (360°/158°) = (180/79)
The number of sides cannot be a fraction
∴ A regular polygon cannot have interior angle 22°
6. (a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Solution:
Interior angle = 180° – Exterior angle
Interior angle is minimum for the polygon having maximum exterior angle
Let the polygon has n sides
Therefore, exterior angle = (360°/n)
Exterior angle is maximum when n is minimum
Minimum number of sides that a polygon can have is 3
Therefore maximum exterior angle = (360°/3) = 120° Answer (b)
Minimum interior angle
= 180° – Maximum exterior angle
= 180° – 120°
= 60° Answer (a)
The next Exercise for NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.3 – Understanding Quadrilaterals can be accessed by clicking here
Download NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.2 – Understanding Quadrilaterals
