NCERT Solutions for Class 8 Maths Chapter 13 Exercise 13.2 Direct and Inverse , has been designed by the NCERT to test the knowledge of the student on the topic Inverse Proportion. Class 8 maths ch 13 ex 13.2 contains 11 questions and each question has explained stepwise. If you are class 8th student you must be looking for the class 8 maths chapter 13 exercise 13.2 solution for your exams preparation. Here we are providing complete NCERT solutions for class 8 maths chapter 13 exercise 13.2.
NCERT solutions for class 8 maths chapter 13 exercise 13.2
Q.1 Which of the following are in inverse proportion?
(i) The number of workers on a job and the time to complete the job.
(ii) The time taken for a journey and the distance travelled in a uniform speed.
(iii) Area of cultivated land and the crop harvested.
(iv) The time taken for a fixed journey and the speed of the vehicle.
(v) The population of a country and the area of land per person.
Solution:
(i) Time taken to complete a job will be less, in case of more workers and more, in case of less workers. So, this in inverse proportion
(ii) As the distance increases, time taken to complete the journey will also increase. So, this is not in inverse proportion
(iii) More crop can be harvested in more area. So, this is not in inverse proportion.
(iv) Time taken to complete a journey will be less when speed of vehicle is more and time taken will be more when speed is less. So, this is in inverse proportion
(v) More land per person in case of less people and less land per person in case of more people. So, this is in inverse proportion
Q.2 In a Television game show, the prize money of Rs 1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners?

Solution:
Unknowns in the given table can be replaced as follows:

The prize amount should be distributed equally among the winners. So, the number of winners and the prize amount given to each winner are inversely proportional to each other
1 × 100000 = 4 × x1
=> x1 = 25000
1 × 100000 = 5 × x2
=> x2 = 20000
1 × 100000 = 8 × x3
=> x3 = 12500
1 × 100000 = 10 × x4
=> x4 = 10000
1 × 100000 = 20 × x5
=> x5 = 5000

Q.3 Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table

(i) Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?
(ii) Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.
(iii) How many spokes would be needed, if the angle between a pair of consecutive spokes is 40°?
Solution:
Unknowns in the given table can be replaced as follows:

Number of spokes and the angle between a pair of consecutive spokes are inversely proportional to each other
4 × 90° = x1 × 8
=> x1 = 45°
4 × 90° = x2 × 8
=> x2 = 36°
4 × 90° = x3 × 8
=> x3 = 30°

(i) Yes
(ii) Let x be the angle between a pair of consecutive spokes on a wheel with 15 spokes
4 × 90° = 15 × x
=> x = (4 × 90°)/15
=> x = 24°
Therefore, the angle between a pair of consecutive spokes of a wheel with 15 spokes is 24°
(iii) Let x be the number of spokes in a wheel
4 × 90° = y × 40°
y = (4 × 90°)/40
=> y = 9
Therefore, the number of spokes if the angle between a pair of consecutive spokes is 40° is 9
Q.4 If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get, if the number of the children is reduced by 4?
Solution:
Given, If a box of sweets is divided among 24 children, they will get 5 sweets each
Number of children is reduced by 4
Number of children = 24 − 4 = 20
Let, x be the number of sweets each student get
The above information can be represented in form of table as below:

Number of students and the number of sweets each student get are inversely proportional to each other
=>24 × 5 = 20 × x
x = (24 × 5)/20
x = 6
Therefore, number of sweets got by each student is 6
Q.5 A farmer has enough food to feed 20 animals in his cattle for 6 days. How long would the food last if there were 10 more animals in his cattle?
Solution:
Given, A farmer has enough food to feed 20 animals in his cattle for 6 days
The above information can be represented in form of table as below:

Number of days the food will last long and the number of animals are inversely proportional to each other
20 × 6 = 30 × x
=> x = (20 × 6)/30
=> x = 4
Therefore, the food would last long for 4 days.
Q.6 A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If, he uses 4 persons instead of three, how long should they take to complete the job?
Solution:
Given, A contractor estimates, 3 persons could rewire Jasminder’s house in 4 days
Let, x be the number of days required to complete the job by 4 persons
The above information can be represented in form of table as below:

Number of days and the number of persons required to complete the job are inversely proportional to each other
4 × 3 = x × 4
=> x = (4 × 3)/4
=> x = 3
Therefore, number of days required to complete the job in 4 days is 3
Q.7 A batch of bottles was packed in 25 boxes with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?
Solution:
Given, A batch of bottles was packed in 25 boxes with 12 bottles in each box
Let, x be the number of boxes filled using 20 bottles in each box
The above information can be represented in form of table as below:

Number of bottles and the number of boxes required to pack these are inversely proportional to each other
12 × 25 = 20 × x
x = (12 × 25)/20
=> x = 15
Therefore, number of boxes required to pack a batch using 20 bottles in each box 15
Q.8 A factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
Solution:
Given, A factory requires 42 machines to produce a given number of articles in 63 days
Let, x be the number of machines required to produce articles in 54 days
The above information can be represented in form of table as below:

Number of machines required and the number of days taken to produce a given number of articles are inversely proportional to each other
42 × 63 = 54× x
=> x = (42 × 63)/54
=> x = 49
Therefore, 49 machines are required to produce given number of articles in 54 days
Q.9 A car takes 2 hours to reach a destination by travelling at the speed of 60 km/h. how long will it take when the car travels at the speed of 80 km/h?
Solution:
Given, A car takes 2 hours to reach destination by travelling at the speed of 60 kmph
Let, x the time taken by the car to reach the destination at a speed of 80kmph
The above information can be represented in form of table as below:
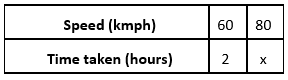
Speed of the car and time taken by car are inversely proportional to each other
60 × 2 = 80 × x
=> x = (60 × 2)/80
=> x = 3/2 hours
=>x = 1 1⁄2 hours
Therefore, time required by the car to reach the destination at 80 kmph is 1 1⁄2 hours.
Q.10 Two persons could fit new windows in house in 3 days.
(i) One of the persons fell ill before the work started. How long would the job take now?
(ii) How many persons would be needed to fit the windows in one day?
Solution:
Given, two persons could fit new windows in house in 3 days
(i) One man fell ill before work started. So, only one person left to work
Let, x be the number of days required by one person to complete the job
The above information can be represented in form of table as below:

Number of persons and the number of days taken to complete the job are inversely proportional to each other
2 × 3 = 1 × x
=> x = 2 x 3
=> x = 6
Therefore, it would take 6 days by one person to fit the windows
(ii) Let, x be the number of persons required to fit the windows in one day
The above information can be represented in form of table as below:

Number of persons and the number of days taken to complete the job are inversely proportional to each other
2 × 3 = x × 1
=> x = 6
Therefore, 6 persons would be needed to fit the windows in one day
Q.11 A school has 8 periods a day each of 45 minutes duration. How long would each period be, if the school has 9 periods a day, assuming the number of school hours to be the same?
Solution:
Given, A school has 8 periods a day each of 45 minutes duration
Let, x be the duration of each period if there are 9 periods a day in the school
The above information can be represented in form of table as below:

Number of periods and duration of each period are inversely proportional to each other
45 × 8 = x × 9
x = (45 × 8)/9
=> x = 40
Therefore, duration of each period will be 40 minutes if school has 9 periods a day
