Arinjay Academy » Maths Class 7 » NCERT Solutions for Class 7 Maths Chapter 2 – Fractions and Decimals

NCERT Solutions for Class 7 Maths Chapter 2 – Fractions and Decimals

Download NCERT Solutions for Class 7 Maths Chapter 2 – Fractions and Decimals – Exercise 2.1, Exercise 2.2, Exercise 2.3, Exercise 2.4, Exercise 2.5, Exercise 2.6, Exercise 2.7

NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.1

1. Solve

i) 2 – $\cfrac { 3 }{ 5 }$

= $\cfrac { 2\times 5 }{ 5 } -\cfrac { 3 }{ 5 }$

= $\cfrac { 10-3 }{ 5 }$

= $\cfrac { 7 }{ 5 }$

ii) 4 + $\cfrac { 7 }{ 8 }$

= $\cfrac { 4\times 8 }{ 8 } +\cfrac { 7 }{ 8 }$

= $\cfrac { 32+7 }{ 8 }$

= $\cfrac { 39 }{ 8 }$

= $4\cfrac { 7 }{ 8 }$

iii) $\cfrac { 3 }{ 5 }$ + $\cfrac { 2 }{ 7 }$

= $\cfrac { 3 }{ 5 } \times \cfrac { 7 }{ 7 } +\cfrac { 2 }{ 7 } \times \cfrac { 5 }{ 5 }$

= $\cfrac { 21+10 }{ 35 }$

= $\cfrac { 31 }{ 35 }$

iv) $\cfrac { 9 }{ 11 }$ – $\cfrac { 4 }{ 15 }$

= $\cfrac { 9 }{ 11 } \times \cfrac { 15 }{ 15 } -\cfrac { 4 }{ 15 } \times \cfrac { 11 }{ 11 }$

= $\cfrac { 135-44 }{ 165 }$

= $\cfrac { 91 }{ 165 }$

v) $\cfrac { 7 }{ 10 }$ + $\cfrac { 2 }{ 5 } +\cfrac { 3 }{ 2 }$

= $\cfrac { 7 }{ 10 } +\cfrac { 2 }{ 5 } \times \cfrac { 2 }{ 2 } +\cfrac { 3 }{ 2 } \times \cfrac { 5 }{ 5 }$

= $\cfrac { 7 }{ 10 }$ + $\cfrac { 4 }{ 10 } + \cfrac { 15 }{ 10 }$

= $\cfrac { 26 }{ 10 }$

= $\cfrac { 13 }{ 5 }$

= $2\cfrac { 3 }{ 5 }$

vi) $2\cfrac { 2 }{ 3 }$ + $3\cfrac { 1 }{ 2 }$

= $\cfrac { 8 }{ 3 }$ + $\cfrac { 7 }{ 2 }$

= $\cfrac { 8 }{ 3 } \times \cfrac { 2 }{ 2 } +\cfrac { 7 }{ 2 } \times \cfrac { 3 }{ 3 }$

= $\cfrac { 16+21 }{ 6 }$

= $\cfrac { 37 }{ 6 }$

= $6\cfrac { 1 }{ 6 }$

vii) $8\cfrac { 1 }{ 2 }$ – $3\cfrac { 5 }{ 8 }$

= $\cfrac { 17 }{ 2 }$ – $\cfrac { 29 }{ 8 }$

= $\cfrac { 17 }{ 2 } \times \cfrac { 4 }{ 4 } -\cfrac { 29 }{ 8 }$

= $\cfrac { 68-29 }{ 8 }$

= $\cfrac { 39 }{ 8 }$

= $4\cfrac { 7 }{ 8 }$

2. Arrange the following in descending order:

i) $\cfrac { 2 }{ 9 }$ , $\cfrac { 2 }{ 3 }$ , $\cfrac { 8 }{ 21 }$

Convert them into like fractions (LCM is 63)

$\cfrac { 2 }{ 9 } \times \cfrac { 7 }{ 7 } =\cfrac { 14 }{ 63 }$

$\cfrac { 2 }{ 3 } \times \cfrac { 21 }{ 21 } =\cfrac { 42 }{ 63 }$

$\cfrac { 8 }{ 21 } \times \cfrac { 3 }{ 3 } =\cfrac { 24 }{ 63 }$

Since 42 > 24 > 14

$\cfrac { 2 }{ 3 }$ > $\cfrac { 8 }{ 21 }$ > $\cfrac { 2 }{ 9 }$

ii) $\cfrac { 1 }{ 5 }$ , $\cfrac { 3 }{ 7 }$ , $\cfrac { 7 }{ 10 }$

Convert them into like fractions (LCM is 70)

$\cfrac { 1 }{ 5 } \times \cfrac { 14 }{ 14 } =\cfrac { 14 }{ 70 }$

$\cfrac { 3 }{ 7 } \times \cfrac { 10 }{ 10 } =\cfrac { 30 }{ 70 }$

$\cfrac { 7 }{ 10 } \times \cfrac { 7 }{ 7 } =\cfrac { 49 }{ 70 }$

Since 49 > 30 > 14

$\cfrac { 7 }{ 10 }$ > $\cfrac { 3 }{ 7 }$ > $\cfrac { 1 }{ 5 }$

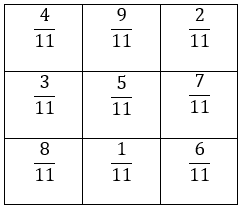
3. In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?

1^st row: $\cfrac { 4 }{ 11 } +\cfrac { 9 }{ 11 } +\cfrac { 2 }{ 11 } =\cfrac { 15 }{ 11 }$

2^nd row: $\cfrac { 3 }{ 11 } +\cfrac { 5 }{ 11 } +\cfrac { 7 }{ 11 } =\cfrac { 15 }{ 11 }$

3^rd row: $\cfrac { 8 }{ 11 } +\cfrac { 1 }{ 11 } +\cfrac { 6 }{ 11 } =\cfrac { 15 }{ 11 }$

1^st column: $\cfrac { 4 }{ 11 } +\cfrac { 3 }{ 11 } +\cfrac { 8 }{ 11 } =\cfrac { 15 }{ 11 }$

2^nd column: $\cfrac { 9 }{ 11 } +\cfrac { 5 }{ 11 } +\cfrac { 1 }{ 11 } =\cfrac { 15 }{ 11 }$

3^rd column: $\cfrac { 2 }{ 11 } +\cfrac { 7 }{ 11 } +\cfrac { 6 }{ 11 } =\cfrac { 15 }{ 11 }$

Diagonal 1: $\cfrac { 4 }{ 11 } +\cfrac { 5 }{ 11 } +\cfrac { 6 }{ 11 } =\cfrac { 15 }{ 11 }$

Diagonal 2: $\cfrac { 2 }{ 11 } +\cfrac { 5 }{ 11 } +\cfrac { 8 }{ 11 } =\cfrac { 15 }{ 11 }$

Therefore, the sum of all the numbers in each row, in each column and along the diagonals is $\cfrac { 15 }{ 11 }$

Hence, it is a magic square.

4. A rectangular sheet of paper is $12\cfrac { 1 }{ 2 }$ cm long and $10\cfrac { 2 }{ 3 }$ cm wide. Find its perimeter.

Given: Length = $12\cfrac { 1 }{ 2 }$ = $\cfrac { 25 }{ 2 }$ cm

Breadth = $10\cfrac { 2 }{ 3 }$ = $\cfrac { 32 }{ 3 }$ cm

Perimeter of a rectangle is = 2(length + breadth)

= 2 $\left[ \cfrac { 25 }{ 2 } +\cfrac { 32 }{ 3 } \right]$

= 2 $\left[ \cfrac { 25 }{ 2 } \times \cfrac { 3 }{ 3 } +\cfrac { 32 }{ 3 } \times \cfrac { 2 }{ 2 } \right]$

= 2 $\left[ \cfrac { 75 }{ 6 } +\cfrac { 64 }{ 6 } \right]$

= 2 x $\cfrac { 139 }{ 6 }$

= $\cfrac { 139 }{ 3 }$

= $46\cfrac { 1 }{ 3 }$

Hence, Perimeter of rectangular sheet of paper is $46\cfrac { 1 }{ 3 }$ cm

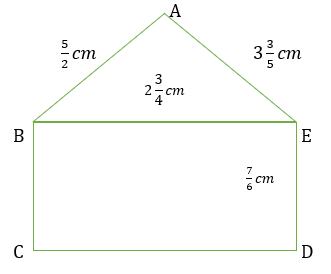
5. Find the perimeters of (i) ∆ABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?

i. Perimeter of ∆ABE = AB + BE + EA

= $\cfrac { 5 }{ 2 }$ + $2\cfrac { 3 }{ 4 }$ + $3\cfrac { 3 }{ 5 }$

= $\cfrac { 5 }{ 2 }$ + $\cfrac { 11 }{ 4 }$ + $\cfrac { 18 }{ 5 }$

= $\cfrac { 5 }{ 2 } \times \cfrac { 10 }{ 10 } +\cfrac { 11 }{ 4 } \times \cfrac { 5 }{ 5 } +\cfrac { 18 }{ 5 } \times \cfrac { 4 }{ 4 }$

= $\cfrac { 50+55+72 }{ 20 }$

= $\cfrac { 177 }{ 20 }$

Perimeter of ∆ABE = $8\cfrac { 17 }{ 20 }$ cm

ii. Perimeter of rectangle = 2(length + breadth)

= 2[BE + ED]

=2 $\left[ 2\cfrac { 3 }{ 4 } +\cfrac { 7 }{ 6 } \right]$

= 2 $\left[\cfrac { 11 }{ 4 } +\cfrac { 7 }{ 6 } \right]$

= 2 $\left[ \cfrac { 11 }{ 4 } \times \cfrac { 3 }{ 3 } +\cfrac { 7 }{ 6 } \times \cfrac { 2 }{ 2 } \right]$

= 2 $\left[\cfrac { 33+14 }{ 12 } \right]$

= 2x $\cfrac { 47 }{ 12 }$

= $\cfrac { 47 }{ 6 }$

= 7 $\cfrac { 5 }{ 6 }$ cm

Converting the perimeters of triangle and rectangle into like fractions (LCM is 60)

$\cfrac { 177 }{ 20 } =\cfrac { 177 }{ 20 } \times \cfrac { 3 }{ 3 } =\cfrac { 531 }{ 60 }$

$\cfrac { 43 }{ 6 } =\cfrac { 43 }{ 6 } \times \cfrac { 10 }{ 10 } =\cfrac { 430 }{ 60 }$

Since 531 > 430

$\cfrac { 177 }{ 20 } >\cfrac { 43 }{ 6 }$

Therefore, the Perimeter of ∆ABE> the perimeter of rectangle BCDE

6. Salil wants to put a picture in a frame. The picture is $7\cfrac { 3 }{ 5 }$ cm wide. To fit in the frame the picture cannot be more than $7\cfrac { 3 }{ 10 }$ cm wide. How much should the picture be trimmed?

Given: Width of the picture = $7\cfrac { 3 }{ 5 }$ = $\cfrac { 38 }{ 5 }$ cm

Required width = $7\cfrac { 3 }{ 10 }$ = $\cfrac { 73 }{ 10 }$ cm

The picture should be trimmed by $\cfrac { 38 }{ 5 }$ – $\cfrac { 73 }{ 10 }$

= $\cfrac { 38 }{ 5 } \times \cfrac { 2 }{ 2 } -\cfrac { 73 }{ 10 }$

= $\cfrac { 76-73 }{ 10 }$

The picture should be trimmed by $\cfrac { 3 }{ 10 }$ cm.

7. Ritu ate $\cfrac { 3 }{ 5 }$ part of an apple and the remaining apple was eaten by her brother Somu.

How much part of the apple did Somu eat? Who had the larger share? By how much?

Given: Part of apple eaten by Ritu = $\cfrac { 3 }{ 5 }$

Part of apple eaten by Somu = 1 – $\cfrac { 3 }{ 5 }$ = $\cfrac { 2 }{ 5 }$

Since 3 > 2, Ritu had the larger share of apple.

Difference between their share is $\cfrac { 3 }{ 5 }$ – $\cfrac { 2 }{ 5 }$ = $\cfrac { 1 }{ 5 }$

Thus, Ritu’s share was larger than Somu’s share by $\cfrac { 1 }{ 5 }$

8. Michael finished colouring a picture in $\cfrac { 7 }{ 12 }$ Vaibhav finished colouring the same picture in $\cfrac { 3 }{ 4 }$ hour. Who worked longer? By what fraction was it longer?

Given: Time taken by Michael = $\cfrac { 7 }{ 12 }$ hour.

Time taken by Vaibhav = $\cfrac { 3 }{ 4 }$ hour

= $\cfrac { 3 }{ 4 } \times \cfrac { 3 }{ 3 } =\cfrac { 9 }{ 12 }$

Since 9 > 7, Vaibhav worked longer.

Difference in their time is $\cfrac { 9 }{ 12 }$ – $\cfrac { 7 }{ 12 }$ = $\cfrac { 1 }{ 6 }$ hour

NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.2

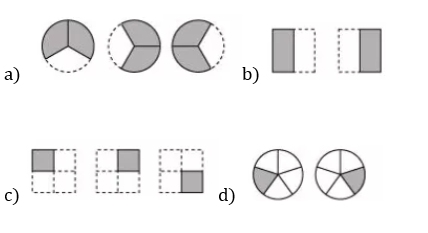
1. Which of the drawings (a) to (d) show:

i) 2 x $\cfrac { 1 }{ 5 }$

Figure d) because it has 2 figures with each representing 1 out of 5 equal parts shaded.

ii) 2 x $\cfrac { 1 }{ 2 }$

Figure b) because it has 2 figures with each having 1 out of 2 equal parts shaded.

iii) 3 x $\cfrac { 2 }{ 3 }$

Figure a) because it has 3 figures with each having 2 out of 3 equal parts shaded.

iv) 3 x $\cfrac { 1 }{ 4 }$

Figure c) because it has 3 figures with each having 1 out of 4 equal parts shaded.

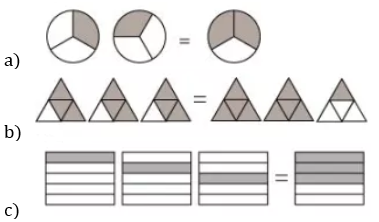
2. Some pictures (a) to (c) are given below. Tell which of them show:

i) 3 x $\cfrac { 1 }{ 5 }$ = $\cfrac { 3 }{ 5 }$

Figure c) since 3 x $\cfrac { 1 }{ 5 }$ represents the addition of 3 figures on the LHS with 1 out of 5 equal parts shaded and $\cfrac { 3 }{ 5 }$ represents 3 out of 5 equal parts shaded on the RHS.

ii) 2 x $\cfrac { 1 }{ 3 }$ = $\cfrac { 2 }{ 3 }$

Figure a) since 2 x $\cfrac { 1 }{ 3 }$ represents the addition of 2 figures on the LHS with 1 out of 3 equal parts shaded and $\cfrac { 2 }{ 3 }$ represents 2 out of 3 equal parts shaded on the RHS.

iii) 3 x $\cfrac { 3 }{ 4 }$ = $2\cfrac { 1 }{ 4 }$

Figure b) since 3 x $\cfrac { 3 }{ 4 }$ represents the addition of 3 figures on the LHS with 3 out of 4 equal parts shaded and $2\cfrac { 1 }{ 4 }$ = 2 + $\cfrac { 1 }{ 4 }$ represents 2 fully shaded figures and 1 out of 4 equal parts shaded on the RHS.

3. Multiply and reduce to lowest form and convert into a mixed fraction:

i) 7 x $\cfrac { 3 }{ 5 }$

= $\cfrac { 21 }{ 5 }$

= $4\cfrac { 1 }{ 5 }$

ii)4 x $\cfrac { 1 }{ 3 }$

= $\cfrac { 4 }{ 3 }$

= $1\cfrac { 1 }{ 3 }$

iii)2 x $\cfrac { 6 }{ 7 }$

= $\cfrac { 12 }{ 7 }$

= $1\cfrac { 5 }{ 7 }$

iv)5 x $\cfrac { 2 }{ 9 }$

= $\cfrac { 10 }{ 9 }$

= $1\cfrac { 1 }{ 9 }$

v) $\cfrac { 2 }{ 3 }$ x 4

= $\cfrac { 8 }{ 3 }$

= $2\cfrac { 2 }{ 3 }$

vi) $\cfrac { 5 }{ 2 }$ x 6

= $\cfrac { 30 }{ 2 }$

= 15

vii)11 x $\cfrac { 4 }{ 7 }$

= $\cfrac { 44 }{ 7 }$

= $6\cfrac { 2 }{ 7 }$

viii) 20 x $\cfrac { 4 }{ 5 }$

= $\cfrac { 80 }{ 5 }$

= 16

ix) 13 x $\cfrac { 1 }{ 3 }$

= $\cfrac { 13 }{ 3 }$

= $4\cfrac { 1 }{ 3 }$

x) 15 x $\cfrac { 3 }{ 5 }$

= $\cfrac { 45 }{ 5 }$

= 9

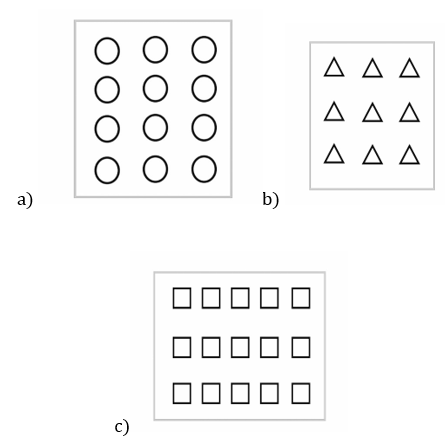
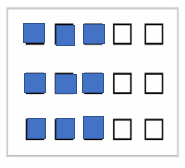
4. Shade:

i) $\cfrac { 1 }{ 2 }$ of the circles in box a)

Here, $\cfrac { 1 }{ 2 }$ x 12 = 6 circles are shaded.

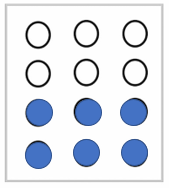
ii) $\cfrac { 2 }{ 3 }$ of the triangles in box b)

Here, $\cfrac { 2 }{ 3 }$ x 9 = 6 triangles are shaded.

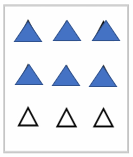
iii) $\cfrac { 3 }{ 5 }$ of the squares in box c)

Here, $\cfrac { 3 }{ 5 }$ x 15 = 9 squares are shaded.

Find:

a) $\cfrac { 1 }{ 2 }$ of

i) 24

$\cfrac { 1 }{ 2 }$ x 24 = 12

ii) 46

$\cfrac { 1 }{ 2 }$ x 46 = 23

b) $\cfrac { 2 }{ 3 }$ of

i) 18

$\cfrac { 2 }{ 3 }$ x 18 = 2 x 6 = 12

ii) 27

$\cfrac { 2 }{ 3 }$ x 27 = 2 x 9 = 18

c) $\cfrac { 3 }{ 4 }$ of

i) 16

$\cfrac { 3 }{ 4 }$ x 16 = 3 x 4 = 12

ii) 36

$\cfrac { 3 }{ 4 }$ x 36 = 3 x 9 = 27

d) $\cfrac { 4 }{ 5 }$ of

i) 20

$\cfrac { 4 }{ 5 }$ x 20 = 4 x 4 = 16

ii) 35

$\cfrac { 4 }{ 5 }$ x 35 = 4 x 7 = 28

6. Multiply and express as a mixed fraction:

a) 3 x $5\cfrac { 1 }{ 5 }$

= 3 x $\cfrac { 26 }{ 5 }$

= $\cfrac { 78 }{ 5 }$

= $15\cfrac { 3 }{ 5 }$

b) 5 x $6\cfrac { 3 }{ 4 }$

= 5 x $\cfrac { 27 }{ 4 }$

= $\cfrac { 135 }{ 4 }$

= $33\cfrac { 3 }{ 4 }$

c) 7 x $2\cfrac { 1 }{ 4 }$

= 7 x $\cfrac { 9 }{ 4 }$

= $\cfrac { 63 }{ 4 }$

= $15\cfrac { 3 }{ 4 }$

d) 4 x $6\cfrac { 1 }{ 3 }$

= 4 x $\cfrac { 19 }{ 3 }$

= $\cfrac { 76 }{ 3 }$

= $25\cfrac { 1 }{ 3 }$

e) $3\cfrac { 1 }{ 4 }$ x 6

= $\cfrac { 13 }{ 4 }$ x 6

= $\cfrac { 78 }{ 4 }$

= $\cfrac { 39 }{ 2 }$

= $19\cfrac { 1 }{ 2 }$

f) $3\cfrac { 2 }{ 5 }$ x 8

= $\cfrac { 17 }{ 5 }$ x 8

= $\cfrac { 136 }{ 5 }$

= $27\cfrac { 1 }{ 5 }$

7. Find

a) $\cfrac { 1 }{ 2 }$ of

i) $2\cfrac { 3 }{ 4 }$

$\cfrac { 1 }{ 2 }$ x $2\cfrac { 3 }{ 4 }$

= $\cfrac { 1 }{ 2 } \times \cfrac { 11 }{ 4 }$

= $\cfrac { 11 }{ 8 }$

= $1\cfrac { 3 }{ 8 }$

ii) $4\cfrac { 2 }{ 9 }$

$\cfrac { 1 }{ 2 }$ x $4\cfrac { 2 }{ 9 }$

= $\cfrac { 1 }{ 2 } \times \cfrac { 38 }{ 9 }$

= $\cfrac { 19 }{ 9 }$

= $2\cfrac { 1 }{ 9 }$

b) $\cfrac { 5 }{ 8 }$ of

i) $3\cfrac { 5 }{ 6 }$

$\cfrac { 5 }{ 8 }$ x $3\cfrac { 5 }{ 6 }$

= $\cfrac { 5 }{ 8 } \times \cfrac { 23 }{ 6 }$

= $\cfrac { 115 }{ 48 }$

= $2\cfrac { 19 }{ 48 }$

ii) $9\cfrac { 2 }{ 3 }$

$\cfrac { 5 }{ 8 }$ x $9\cfrac { 2 }{ 3 }$

= $\cfrac { 5 }{ 8 } \times \cfrac { 29 }{ 3 }$

= $\cfrac { 145 }{ 24 }$

= $6\cfrac { 1 }{ 24 }$

8. Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidhya consumed $\cfrac { 2 }{ 5 }$ of the water. Pratap consumed the remaining water.

i) How much water did Vidya drink?

ii) What fraction of the total quantity of water did Pratap drink?

Given: Volume of water in the bottle = 5 litres

i. Water consumed by Vidhya = $\cfrac { 2 }{ 5 }$ x 5 litres

Water consumed by Vidhya = 2 litres

ii. Fraction of water consumed by Pratap = 1 – $\cfrac { 2 }{ 5 }$

Fraction of water consumed by Pratap = $\cfrac { 3 }{ 5 }$ of total water

NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.3

1. Find:

i) $\cfrac { 1 }{ 4 }$ of

a) $\cfrac { 1 }{ 4 }$

$\cfrac { 1 }{ 4 }$ x $\cfrac { 1 }{ 4 }$ = $\cfrac { 1 }{ 16 }$

b) $\cfrac { 3 }{ 5 }$

$\cfrac { 1 }{ 4 }$ x $\cfrac { 3 }{ 5 }$ = $\cfrac { 3 }{ 20 }$

c) $\cfrac { 1 }{ 4 }$

$\cfrac { 1 }{ 4 }$ x $\cfrac { 4 }{ 3 }$ = $\cfrac { 1 }{ 3 }$

ii) $\cfrac { 1 }{ 7 }$ of

a) $\cfrac { 2 }{ 9 }$

$\cfrac { 1 }{ 7 }$ x $\cfrac { 2 }{ 9 }$ = $\cfrac { 2 }{ 63 }$

b) $\cfrac { 6 }{ 5 }$

$\cfrac { 1 }{ 7 }$ x $\cfrac { 6 }{ 5 }$ = $\cfrac { 6 }{ 35 }$

c) $\cfrac { 3 }{ 10 }$

$\cfrac { 1 }{ 7 }$ x $\cfrac { 3 }{ 10 }$ = $\cfrac { 3 }{ 70 }$

2. Multiply and reduce to lowest form (if possible) :

i) $\cfrac { 2 }{ 3 }$ x $2\cfrac { 2 }{ 3 }$

= $\cfrac { 2 }{ 3 }$ x $\cfrac { 8 }{ 3 }$

= $\cfrac { 16 }{ 9 }$

= $1\cfrac { 7 }{ 9 }$

ii) $\cfrac { 2 }{ 7 }$ x $\cfrac { 7 }{ 9 }$

= $\cfrac { 2 }{ 9 }$

iii) $\cfrac { 3 }{ 8 }$ x $\cfrac { 6 }{ 4 }$

= $\cfrac { 3 }{ 8 }$ x $\cfrac { 3 }{ 2 }$

= $\cfrac { 9 }{ 16 }$

iv) $\cfrac { 9 }{ 5 }$ x $\cfrac { 3 }{ 5 }$

= $\cfrac { 27 }{ 25 }$

= $1\cfrac { 2 }{ 25 }$

v) $\cfrac { 1 }{ 3 }$ x $\cfrac { 15 }{ 8 }$

= $\cfrac { 5 }{ 8 }$

vi) $\cfrac { 11 }{ 2 }$ x $\cfrac { 3 }{ 10 }$

= $\cfrac { 33 }{ 20 }$

= $1\cfrac { 13 }{ 20 }$

vii) $\cfrac { 4 }{ 5 }$ x $\cfrac { 12 }{ 7 }$

= $\cfrac { 48 }{ 35 }$

= $1\cfrac { 13 }{ 35 }$

3. Multiply the following fractions:

i) $\cfrac { 2 }{ 5 }$ x $5\cfrac { 1 }{ 4 }$

= $\cfrac { 2 }{ 5 }$ x $\cfrac { 21 }{ 4 }$

= $\cfrac { 21 }{ 10 }$

= $2\cfrac { 1 }{ 10 }$

ii) $6\cfrac { 2 }{ 5 }$ x $\cfrac { 7 }{ 9 }$

= $\cfrac { 32 }{ 5 }$ x $\cfrac { 7 }{ 9 }$

= $\cfrac { 224 }{ 45 }$

= $4\cfrac { 44 }{ 45 }$

iii) $\cfrac { 3 }{ 2 }$ x $5\cfrac { 1 }{ 3 }$

= $\cfrac { 3 }{ 2 }$ x $\cfrac { 16 }{ 3 }$

= 8

iv) $\cfrac { 5 }{ 6 }$ x $2\cfrac { 3 }{ 7 }$

= $\cfrac { 5 }{ 6 }$ x $\cfrac { 17 }{ 7 }$

= $\cfrac { 85 }{ 42 }$

= $2\cfrac { 1 }{ 42 }$

v) $3\cfrac { 2 }{ 5 }$ x $\cfrac { 4 }{ 7 }$

= $\cfrac { 17 }{ 5 }$ x $\cfrac { 4 }{ 7 }$

= $\cfrac { 68 }{ 35 }$

= $1\cfrac { 33 }{ 35 }$

vi) $2\cfrac { 3 }{ 5 }$ x 3

= $\cfrac { 13 }{ 5 }$ x 3

= $\cfrac { 39 }{ 5 }$

= $7\cfrac { 4 }{ 5 }$

vii) $3\cfrac { 4 }{ 7 }$ x $\cfrac { 3 }{ 5 }$

= $\cfrac { 25 }{ 7 }$ x $\cfrac { 3 }{ 5 }$

= $\cfrac { 15 }{ 7 }$

= $2\cfrac { 1 }{ 7 }$

4. Which is greater:

i) $\cfrac { 2 }{ 7 }$ of $\cfrac { 3 }{ 4 }$ or $\cfrac { 3 }{ 5 }$ of $\cfrac { 5 }{ 8 }$

$\cfrac { 2 }{ 7 }$ of $\cfrac { 3 }{ 4 }$ = $\cfrac { 2 }{ 7 }$ x $\cfrac { 3 }{ 4 }$

= $\cfrac { 3 }{ 14 }$

$\cfrac { 3 }{ 5 }$ of $\cfrac { 5 }{ 8 }$ = $\cfrac { 3 }{ 5 }$ x $\cfrac { 5 }{ 8 }$

= $\cfrac { 3 }{ 8 }$

$\cfrac { 3 }{ 14 }$ ? $\cfrac { 3 }{ 8 }$

Convert them into like fractions (LCM is 56)

$\cfrac { 3 }{ 14 }$ x $\cfrac { 4 }{ 4 }$ = $\cfrac { 12 }{ 56 }$

$\cfrac { 3 }{ 8 }$ x $\cfrac { 7 }{ 7 }$ = $\cfrac { 21 }{ 56 }$

Since 21 > 12

$\cfrac { 3 }{ 8 }$ > $\cfrac { 3 }{ 14 }$

Therefore, $\cfrac { 3 }{ 5 }$ of $\cfrac { 5 }{ 8 }$ is greater.

ii) $\cfrac { 1 }{ 2 }$ of $\cfrac { 6 }{ 7 }$ or $\cfrac { 2 }{ 3 }$ of $\cfrac { 3 }{ 7 }$

$\cfrac { 1 }{ 2 }$ of $\cfrac { 6 }{ 7 }$ = $\cfrac { 1 }{ 2 }$ x $\cfrac { 6 }{ 7 }$

= $\cfrac { 3 }{ 7 }$

$\cfrac { 2 }{ 3 }$ of $\cfrac { 3 }{ 7 }$ = $\cfrac { 2 }{ 3 }$ x $\cfrac { 3 }{ 7 }$

= $\cfrac { 2 }{ 7 }$

Since, 3 > 2

$\cfrac { 3 }{ 7 }$ > $\cfrac { 2 }{ 7 }$

Therefore, $\cfrac { 1 }{ 2 }$ of $\cfrac { 6 }{ 7 }$ is greater.

5. Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is $\cfrac { 3 }{ 4 }$ m . Find the distance between the first and the last sapling.

From the figure, the distance between the first and the last sapling is equal to 3 x $\cfrac { 3 }{ 4 }$ = $\cfrac { 9 }{ 4 }$ = $2\cfrac { 1 }{ 4 }$ m.

6. Lipika reads a book for $1\cfrac { 3 }{ 4 }$ hours every day. She reads the entire book in 6 days. How many hours in all were required by her to read the book?

Given: Number hours Lipika reads the book every day= $1\cfrac { 3 }{ 4 }$

Number of days taken to read the book = 6

Total number of hours Lipika takes to read the entire book = $1\cfrac { 3 }{ 4 }$ x 6

= $\cfrac { 7 }{ 4 }$ x 6

= $\cfrac { 21 }{ 2 }$

= $10\cfrac { 1 }{ 2 }$

Time taken by Lipika to read the entire book is $10\cfrac { 1 }{ 2 }$ hours.

7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using $2\cfrac { 3 }{ 4 }$ litres of petrol?

Given: Distance covered by car in 1 litre of petrol = 16km

Distance covered by car in litres of petrol = 16 x $2\cfrac { 3 }{ 4 }$

= 16 x $\cfrac { 11 }{ 4 }$

= 44 km

Thus, the car will cover 44km using $2\cfrac { 3 }{ 4 }$ litres of petrol.

8. a) i) Provide the number in the box $\boxed { }$ , such that

$\cfrac { 2 }{ 3 }$ x $\boxed { }$ = $\cfrac { 10 }{ 30 }$

$\cfrac { 2 }{ 3 }$ x $\boxed { \cfrac { 5 }{ 10 } }$ = $\cfrac { 10 }{ 30 }$

ii) The simplest form of the number obtained in $\boxed { }$ is ___.

Ans: $\cfrac { 5 }{ 10 }$ = $\cfrac { 1 }{ 2 }$

b) i) Provide the number in the box $\boxed { }$ , such that

$\cfrac { 3 }{ 5 }$ x $\boxed { }$ = $\cfrac { 24 }{ 75 }$

$\cfrac { 3 }{ 5 }$ x $\boxed { \cfrac { 8 }{ 15 } }$ = $\cfrac { 24 }{ 75 }$

ii) The simplest form of the number obtained in $\boxed { }$ is, _________.

$\cfrac { 8 }{ 15 }$ cannot be further simplified.

NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.4

1. Find:

i) 12 ÷ $\cfrac { 3 }{ 4 }$

= 12 x $\cfrac { 4 }{ 3 }$

= 16

ii) 14 ÷ $\cfrac { 5 }{ 6 }$

= 14 x $\cfrac { 6 }{ 5 }$

= $\cfrac { 84 }{ 5 }$

iii) 8 ÷ $\cfrac { 7 }{ 3 }$

= 8 x $\cfrac { 3 }{ 7 }$

= $\cfrac { 24 }{ 7 }$

iv) 4 ÷ $\cfrac { 8 }{ 3 }$

= 4 x $\cfrac { 3 }{ 8 }$

= $\cfrac { 3 }{ 2 }$

v) 3 ÷ $2\cfrac { 1 }{ 3 }$

= 3 ÷ $\cfrac { 7 }{ 3 }$

= 3 x $\cfrac { 3 }{ 7 }$

= $\cfrac { 9 }{ 7 }$

vi) 5 ÷ $3\cfrac { 4 }{ 7 }$

= 5 ÷ $\cfrac { 25 }{ 7 }$

= 5 x $\cfrac { 7 }{ 25 }$

= $\cfrac { 7 }{ 5 }$

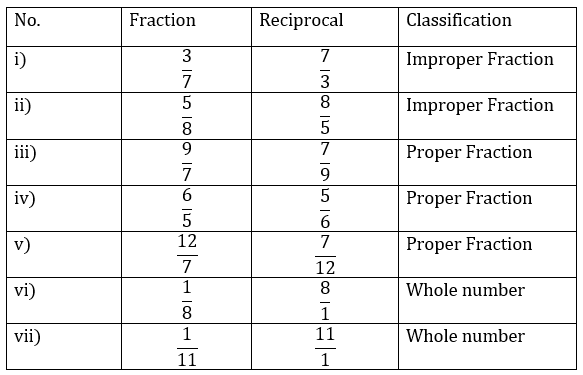
2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.

Note:

Proper Fractions: A fraction that is less than one, with the numerator less than the denominator.
Improper Fractions: A fraction in which the numerator is greater than its denominator
Whole Numbers: Collection of all positive integers, including 0

3. Find:

i) $\cfrac { 7 }{ 3 }$ ÷ 2

= $\cfrac { 7 }{ 3 }$ ÷ $\cfrac { 2 }{ 1 }$

= $\cfrac { 7 }{ 3 }$ x $\cfrac { 1 }{ 2 }$

= $\cfrac { 7 }{ 6 }$

ii) $\cfrac { 4 }{ 9 }$ ÷ 5

= $\cfrac { 4 }{ 9 }$ ÷ $\cfrac { 5 }{ 1 }$

= $\cfrac { 4 }{ 9 }$ x $\cfrac { 1 }{ 5 }$

= $\cfrac { 4 }{ 45 }$

iii) $\cfrac { 6 }{ 13 }$ ÷ 7

= $\cfrac { 6 }{ 13 }$ ÷ $\cfrac { 7 }{ 1 }$

= $\cfrac { 6 }{ 13 }$ x $\cfrac { 1 }{ 7 }$

= $\cfrac { 6 }{ 91 }$

iv) $4\cfrac { 1 }{ 3 }$ ÷ 3

= $\cfrac { 13 }{ 3 }$ ÷ $\cfrac { 3 }{ 1 }$

= $\cfrac { 13 }{ 3 }$ x $\cfrac { 1 }{ 3 }$

= $\cfrac { 13 }{ 9 }$

v) $3\cfrac { 1 }{ 2 }$ ÷ 4

= $\cfrac { 7 }{ 2 }$ ÷ $\cfrac { 4 }{ 1 }$

= $\cfrac { 7 }{ 2 }$ x $\cfrac { 1 }{ 4 }$

= $\cfrac { 7 }{ 8 }$

vi) $4\cfrac { 3 }{ 7 }$ ÷ 7

= $\cfrac { 31 }{ 7 }$ ÷ $\cfrac { 7 }{ 1 }$

= $\cfrac { 31 }{ 7 }$ x $\cfrac { 1 }{ 7 }$

= $\cfrac { 31 }{ 49 }$

4. Find:

i) $\cfrac { 2 }{ 5 }$ ÷ $\cfrac { 1 }{ 2 }$

= $\cfrac { 2 }{ 5 }$ x $\cfrac { 2 }{ 1 }$

= $\cfrac { 4 }{ 5 }$

ii) $\cfrac { 4 }{ 9 }$ ÷ $\cfrac { 2 }{ 3 }$

= $\cfrac { 4 }{ 9 }$ x $\cfrac { 3 }{ 2 }$

= $\cfrac { 2 }{ 3 }$

iii) $\cfrac { 3 }{ 7 }$ ÷ $\cfrac { 8 }{ 7 }$

= $\cfrac { 3 }{ 7 }$ x $\cfrac { 7 }{ 8 }$

= $\cfrac { 3 }{ 8 }$

iv) $2\cfrac { 1 }{ 3 }$ ÷ $\cfrac { 3 }{ 5 }$

= $\cfrac { 7 }{ 3 }$ ÷ $\cfrac { 3 }{ 5 }$

= $\cfrac { 7 }{ 3 }$ x $\cfrac { 5 }{ 3 }$

= $\cfrac { 35 }{ 9 }$

v) $3\cfrac { 1 }{ 2 }$ ÷ $\cfrac { 8 }{ 3 }$

= $\cfrac { 7 }{ 2 }$ ÷ $\cfrac { 8 }{ 3 }$

= $\cfrac { 7 }{ 2 }$ x $\cfrac { 3 }{ 8 }$

= $\cfrac { 21 }{ 16 }$

vi) $\cfrac { 2 }{ 5 }$ ÷ $1\cfrac { 1 }{ 2 }$

= $\cfrac { 2 }{ 5 }$ ÷ $\cfrac { 3 }{ 2 }$

= $\cfrac { 2 }{ 5 }$ x $\cfrac { 2 }{ 3 }$

= $\cfrac { 4 }{ 15 }$

vii) $3\cfrac { 1 }{ 5 }$ ÷ $1\cfrac { 2 }{ 3 }$

= $\cfrac { 16 }{ 5 }$ ÷ $\cfrac { 5 }{ 3 }$

= $\cfrac { 16 }{ 5 }$ x $\cfrac { 3 }{ 5 }$

= $\cfrac { 48 }{ 25 }$

viii) $2\cfrac { 1 }{ 5 }$ ÷ $1\cfrac { 1 }{ 5 }$

= $\cfrac { 11 }{ 5 }$ ÷ $\cfrac { 6 }{ 5 }$

= $\cfrac { 11 }{ 5 }$ x $\cfrac { 5 }{ 6 }$

= $\cfrac { 11 }{ 6 }$

NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.5

1. Which is greater?

i) 0.5 or 0.05

0.5 = $\cfrac { 5 }{ 10 }$ = $\cfrac { 5\times 10 }{ 10\times 10 }$ = $\cfrac { 50 }{ 100 }$

0.05 = $\cfrac { 5 }{ 100 }$

50 > 5

Therefore, 0.5 > 0.05

ii) 0.7 or 0.5

0.7 = $\cfrac { 7 }{ 10 }$

0.5 = $\cfrac { 5 }{ 10 }$

7 > 5

Therefore, 0.7 > 0.5

iii) 7 or 0.7

7 = $\cfrac { 7 }{ 1 }$ = $\cfrac { 7\times 10 }{ 1\times 10 }$ = $\cfrac { 70 }{ 10 }$

0.7 = $\cfrac { 7 }{ 10 }$

70 > 7

Therefore, 7 > 0.7

iv) 1.37 or 1.49

1.37 = $\cfrac { 137 }{ 100 }$

1.49 = $\cfrac { 149 }{ 100 }$

137 < 149

Therefore, 1.37 < 1.49

v) 2.03 or 2.30

2.03 = $\cfrac { 203 }{ 100 }$

2.30 = $\cfrac { 230 }{ 100 }$

203 < 230

Therefore, 2.03 < 2.30

vi) 0.8 or 0.88

0.8 = $\cfrac { 8 }{ 10 }$ = = $\cfrac { 8\times 10 }{ 10\times 10 }$ = $\cfrac { 80 }{ 100 }$

0.88 = $\cfrac { 88 }{ 100 }$

80 < 88

Therefore, 0.8 < 0.88

2. Express as rupees using decimals:

Note: ₹ 1 = 100 paise. To convert paise into rupees, divide paise by 100

i) 7 paise

7 paise = ₹ $\cfrac { 7 }{ 100 }$ = ₹0.07

ii) 7 rupees 7 paise

₹7 + ₹ $\cfrac { 7 }{ 100 }$

= 7 + 0.07

= ₹ 7.07

iii) 77 rupees 77 paise

₹77 + ₹ $\cfrac { 77 }{ 100 }$

= 77 + 0.77

= ₹ 77.77

iv) 50 paise

50 paise = ₹ $\cfrac { 50 }{ 100 }$ = ₹0.5

v) 235 paise

235 paise = ₹ $\cfrac { 235 }{ 100 }$ = ₹ 2.35

3) (i) Express 5 cm in metre and kilometre

5cm = $\cfrac { 5 }{ 100 }$ m = 0.05 m

5cm = $\cfrac { 5 }{ 100 }$ x $\cfrac { 1 }{ 1000 }$ = $\cfrac { 5 }{ 100000 }$ = 0.00005 km

(ii) Express 35 mm in cm, m and km

35mm = $\cfrac { 35 }{ 10 }$ cm = 3.5 cm

35mm = $\cfrac { 35 }{ 1000 }$ m = 0.035 m

35mm = $\cfrac { 35 }{ 1000000 }$ km = 0.000035 km

4) Express in kg:

Note: 1 kg = 1000 g

To convert grams to kilograms, divide grams by 1000

i) 200 g

200 g= $\cfrac { 200 }{ 1000 }$ kg

= 0.2 kg

ii) 3470 g

3470 g = $\cfrac { 3470 }{ 1000 }$ kg

= 0.347 kg

iv) 4 kg 8 g

4 kg + $\cfrac { 8 }{ 1000 }$ kg

= 4 + 0.008 kg

= 4.008 kg

5) Write the following decimal numbers in the expanded form:

i) 20.03 = 2 x 10 + 0 x 1 + 0 x $\cfrac { 1 }{ 10 }$ + 3 x $\cfrac { 1 }{ 100 }$

ii) 2.03 = 2 x 1 + 0 x $\cfrac { 1 }{ 10 }$ + 3 x $\cfrac { 1 }{ 100 }$

iii) 200.03 = 2 x 100 + 0 x 10 + 0 x 1 + 0 x $\cfrac { 1 }{ 10 }$ + 3 x $\cfrac { 1 }{ 100 }$

iv)2.034 = 2 x 1 + 0 x $\cfrac { 1 }{ 10 }$ + 3 x $\cfrac { 1 }{ 100 }$ + 4 x $\cfrac { 1 }{ 1000 }$

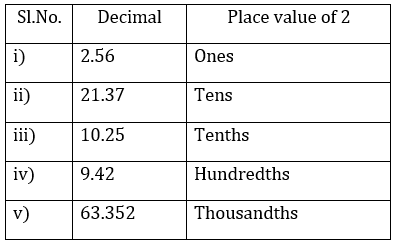
6) Write the place value of 2 in the following decimal numbers:

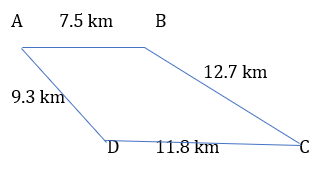
7. Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?

Distance travelled by Dinesh = AB + BC

Distance travelled by Dinesh = 7. 5 km + 12.7 km

Distance travelled by Dinesh = 20.2 km

Distance travelled by Ayub = AD + DC

Distance travelled by Ayub = 9.3 km + 11.8 km

Distance travelled by Ayub = 21.1 km

Therefore, Ayub travelled more distance.

Difference = 21.1 km – 20.2 km = 0.9 km

8) Shyama bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?

Fruits bought by Shyama = 5 kg 300 g + 3 kg + 250 g

= 5 kg + $\cfrac { 300 }{ 1000 }$ kg + 3 kg + $\cfrac { 250 }{ 1000 }$ kg

= 8 + 0.3 + 0.25

= 8.55 kg

Fruits bought by Sarala = 4 kg 800 g + 4 kg 150 g

= 4 kg + $\cfrac { 800 }{ 1000 }$ kg + 4 kg + $\cfrac { 150 }{ 1000 }$ kg

= 8 + 0.8 + 0.15

= 8.95 kg

Therefore, Sarala bought more fruits.

9) How much less is 28 km than 42.6 km?

42.6 km – 28 km = 14.6 km

Therefore, 28 km is 14.6 km less than 42.6 km.

NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.6

1. Find

i) 0.2 x 6

= $\cfrac { 2 }{ 10 }$ x 6

= $\cfrac { 12 }{ 10 }$

= 1.2

ii) 8 x 4.6

= 8 x $\cfrac { 46 }{ 10 }$

= $\cfrac { 368 }{ 10 }$

= 36.8

iii) 2.71 x 5

= $\cfrac { 271 }{ 100 }$ x 5

= $\cfrac { 1355 }{ 100 }$

= 13.55

iv) 20.1 x 4

= $\cfrac { 201 }{ 10 }$ x 4

= $\cfrac { 804 }{ 10 }$

= 80.4

v) 0.05 x 7

= $\cfrac { 5 }{ 100 }$ x 7

= $\cfrac { 35 }{ 100 }$

= 0.35

vi) 211.02 x 4

= $\cfrac { 21102 }{ 100 }$ x 4

= $\cfrac { 84408 }{ 100 }$

= 844.08

vii) 2 x 0.86

= 2 x $\cfrac { 86 }{ 100 }$

= $\cfrac { 172 }{ 100 }$

= 1.72

2. Find the area of rectangle whose length is 5.7cm and breadth is 3 cm.

Given: Length = 5.7 cm

Breadth = 3 cm

Area of rectangle = Length x Breadth

= 5.7 cm x 3 cm

= 1.71 cm²

3. Find:

Note: When a decimal number is multiplied by 10, 100 or 1000, the digits in the product are same as in the decimal number but the decimal point in the product is shifted to the right by as, many of places as there are zeros.

i) 1.3 x 10 = 13

ii) 36.8 x 10 = 368

iii) 153.7 x 10 = 1537

iv) 168.07 x 10 = 1680.7

v) 31.1 x 100 = 3110

vi) 156.1 x 100 = 15610

vii) 3.62 x 100 = 362

viii) 43.07 x 100 = 4307

ix) 0.5 x 10 = 5

x) 0.08 x 10 = 0.8

xi) 0.9 x 100 = 90

xii) 0.03 x 1000 = 30

4. A two-wheeler covers a distance of 55.3 km in one litre of petrol. How much distance will it cover in 10 litres of petrol?

Given: Distance covered in 1 litre of petrol = 55.3 km

Distance covered in 10 litres of petrol = 55.3 x 10 = 553 km

5. Find:

i) 2.5 x 0.3

= $\cfrac { 25 }{ 10 }$ x $\cfrac { 3 }{ 10 }$

= $\cfrac { 75 }{ 100 }$

= 0.75

ii) 0.1 x 51.7

= $\cfrac { 1 }{ 10 }$ x $\cfrac { 517 }{ 10 }$

= $\cfrac { 517 }{ 100 }$

= 5.17

iii) 0.2 x 316.8

= $\cfrac { 2 }{ 10 }$ x $\cfrac { 3168 }{ 10 }$

= $\cfrac { 6336 }{ 100 }$

= 63.36

iv) 1.3 x 3.1

= $\cfrac { 13 }{ 10 }$ x $\cfrac { 31 }{ 10 }$

= $\cfrac { 403 }{ 100 }$

= 4.03

v) 0.5 x 0.05

= $\cfrac { 5 }{ 10 }$ x $\cfrac { 5 }{ 100 }$

= $\cfrac { 25 }{ 1000 }$

= 0.025

vi) 11.2 x 0.15

= $\cfrac { 112 }{ 10 }$ x $\cfrac { 15 }{ 100 }$

= $\cfrac { 1680 }{ 1000 }$

= 1.68

vii) 1.07 x 0.02

= $\cfrac { 107 }{ 100 }$ x $\cfrac { 2 }{ 100 }$

= $\cfrac { 214 }{ 10000 }$

= 0.0214

viii) 10.05 x 1.05

= $\cfrac { 1005 }{ 100 }$ x $\cfrac { 105 }{ 100 }$

= $\cfrac { 105525 }{ 10000 }$

= 10.5525

ix) 101.01 x 0.01

= $\cfrac { 10101 }{ 100 }$ x $\cfrac { 1 }{ 100 }$

= $\cfrac { 10101 }{ 10000 }$

= 1.0101

x) 100.01 x 1.1

= $\cfrac { 10001 }{ 100 }$ x $\cfrac { 11 }{ 10 }$

= $\cfrac { 110011 }{ 1000 }$

= 110.011

NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.7

1. Find:

i) 0.4 ÷ 2

= $\cfrac { 4 }{ 10 }$ ÷ $\cfrac { 2 }{ 1 }$

= $\cfrac { 4 }{ 10 }$ x $\cfrac { 1 }{ 2 }$

= $\cfrac { 2 }{ 10 }$

= 0.2

ii) 0.35 ÷ 5

= $\cfrac { 35 }{ 100 }$ ÷ $\cfrac { 5 }{ 1 }$

= $\cfrac { 35 }{ 100 }$ x $\cfrac { 1 }{ 5 }$

= $\cfrac { 7 }{ 100 }$

= 0.07

iii) 2.48 ÷ 4

= $\cfrac { 248 }{ 100 }$ ÷ $\cfrac { 4 }{ 1 }$

= $\cfrac { 248 }{ 100 }$ x $\cfrac { 1 }{ 4 }$

= $\cfrac { 62 }{ 100 }$

= 0.62

iv) 65.4 ÷ 6

= $\cfrac { 654 }{ 10 }$ ÷ $\cfrac { 6 }{ 1 }$

= $\cfrac { 654 }{ 10 }$ x $\cfrac { 1 }{ 6 }$

= $\cfrac { 109 }{ 10 }$

= 10.9

v) 651.2 ÷ 4

= $\cfrac { 6512 }{ 10 }$ ÷ $\cfrac { 4 }{ 1 }$

= $\cfrac { 6512 }{ 10 }$ x $\cfrac { 1 }{ 4 }$

= $\cfrac { 1628 }{ 10 }$

= 162.8

vi) 14.49 ÷ 7

= $\cfrac { 1449 }{ 100 }$ ÷ $\cfrac { 7 }{ 1 }$

= $\cfrac { 1449 }{ 100 }$ x $\cfrac { 1 }{ 7 }$

= $\cfrac { 207 }{ 100 }$

= 20.7

vii) 3.96 ÷ 4

= $\cfrac { 396 }{ 100 }$ ÷ $\cfrac { 4 }{ 1 }$

= $\cfrac { 396 }{ 100 }$ x $\cfrac { 1 }{ 4 }$

= $\cfrac { 99 }{ 100 }$

= 0.99

viii) 0.80 ÷ 5

= $\cfrac { 80 }{ 100 }$ ÷ $\cfrac { 5 }{ 1 }$

= $\cfrac { 80 }{ 100 }$ x $\cfrac { 1 }{ 5 }$

= $\cfrac { 16 }{ 100 }$

= 0.16

2. Find:

Note: While dividing a number by 10 the digits of the number and the quotient are same but the decimal point in the quotient shifts to the left by one place

i) 4.8 ÷ 10 = 0. 48

ii) 52.5 ÷ 10 = 5.25

iii) 0.7 ÷ 10 = 0.07

iv) 33.1 ÷ 10 = 3.31

v) 272.23 ÷ 10 = 27.223

vi) 0.56 ÷ 10 = 0.056

vii) 3.97 ÷ 10 = 0.397

3. Find:

Note: While dividing a number by 100 the digits of the number and the quotient are same but the decimal point in the quotient shifts to the left by two places.

i) 2.7 ÷ 100 = 0.027

ii) 0.3 ÷ 100 = 0.003

iii) 0.78 ÷ 100 = 0.0078

iv) 432.6 ÷ 100 = 4.326

v) 23.6 ÷ 100 = 0.236

vi) 98.53 ÷ 100 = 0.9853

4. Find:

Note: While dividing a number by 1000 the digits of the number and the quotient are same but the decimal point in the quotient shifts to the left by three places.

i) 7.9 ÷ 1000 = 0.0079

ii) 26.3 ÷ 1000 = 0.0263

iii) 38.53 ÷ 1000 = 0.03853

iv) 128.9 ÷ 1000 = 0.1289

v) 0.5 ÷ 1000 = 0.0005

5. Find:

i) 7 ÷ 3.5

= 7÷ $\cfrac { 35 }{ 10 }$

= 7 x $\cfrac { 10 }{ 35 }$