Download NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.1 – Pair of Linear Equations in two Variables. This Exercise contains 3 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 10 for Maths NCERT solutions for other Chapters, you can click the link at the end of this Note.
NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.1 – Pair of Linear Equations in two Variables


NCERT Solutions For Class 10 Maths Chapter 3 Exercise 3.1 – Pair of Linear Equations in two Variables
1. Aftab tells his daughter, “seven years ago, I was 7 times as old as you were then. Also three years from now, I shall be three times as old as you will be”. (Isn’t this interesting?) Represent this situation algebraically and graphically.
Solution:
Let Aftab and his daughter’s present age be x and y years respectively.
Then 7 years ago,
Aftab’s age = (x-7)
His daughter’s age = (y-7)
Therefore,
(x-7) = 7(y-7)
x – 7 = 7y – 49
x = 7y – 42
x – 7y + 42 = 0 ….(i)
And after 3 years,
Aftab’s age = (x+3)
His daughter’s age = (y+3)
Therefore,
(x+3) = 3(y+3)
x + 3 = 3y + 9
x = 3y + 6
x – 3y – 6 = 0 ….(ii)
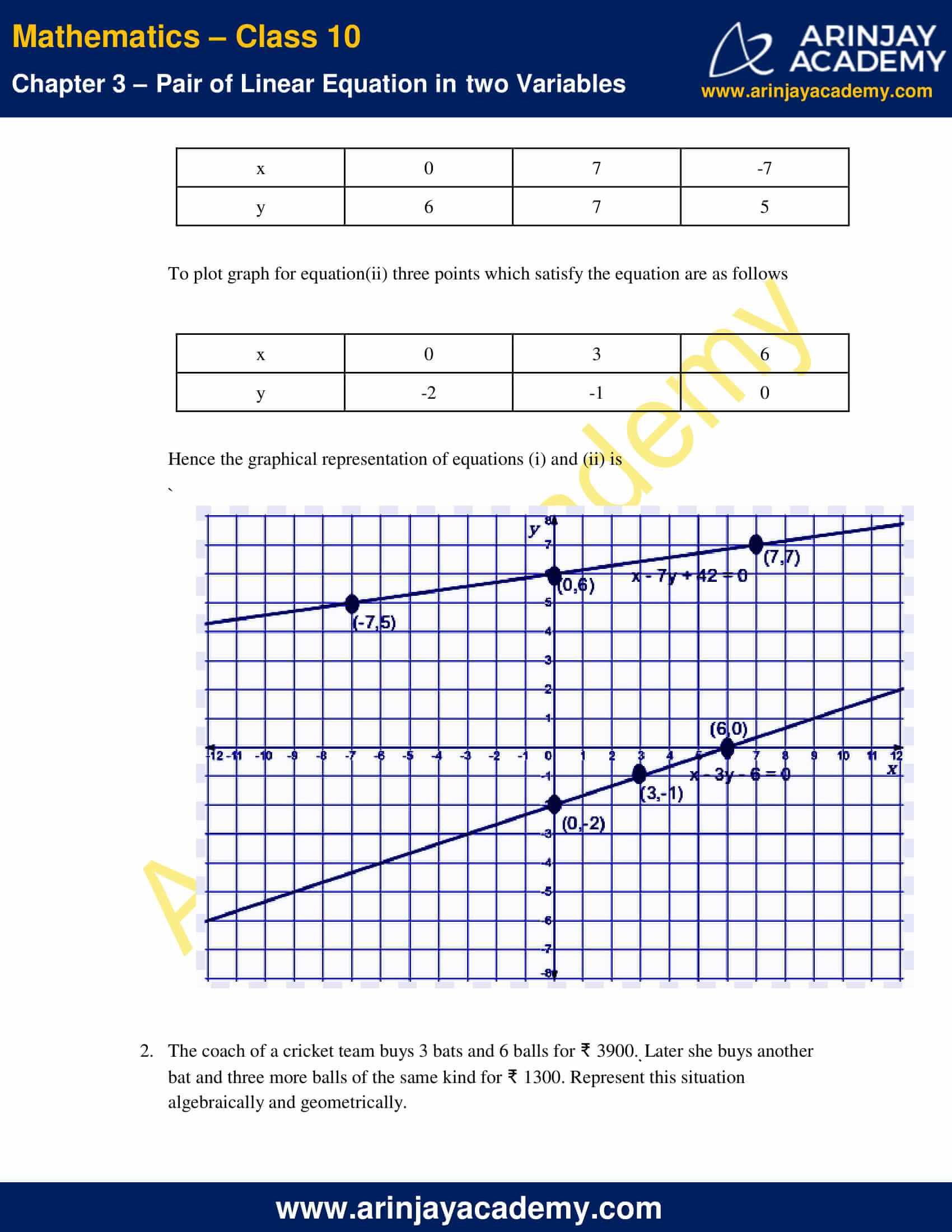
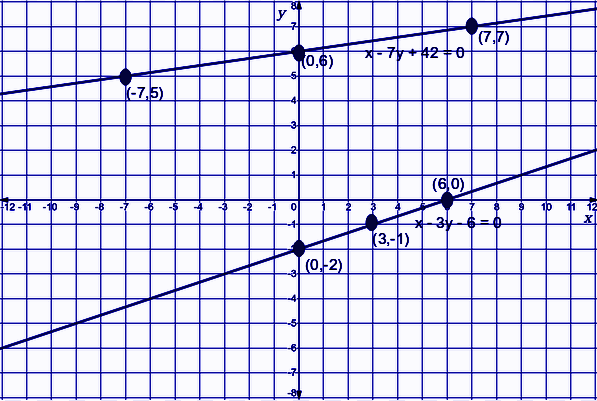
To plot graph for equation(i) three points which satisfy the equation are as follows

To plot graph for equation(ii) three points which satisfy the equation are as follows

Hence the graphical representation of equations (i) and (ii) is
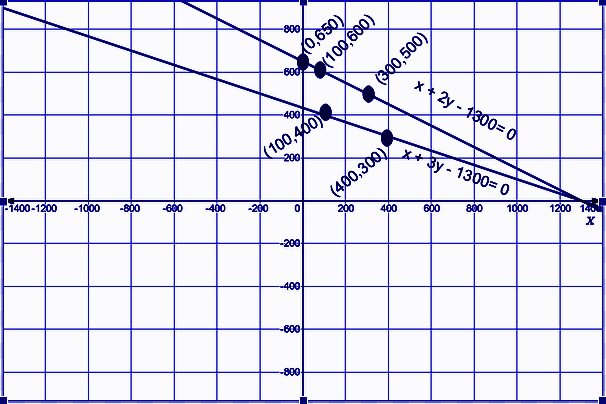
2. The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later she buys another bat and three more balls of the same kind for ₹ 1300. Represent this situation algebraically and geometrically.
Solution:
Let x be the cost of each bat and y be the cost of each ball.
From the given condition,
3x+6y = 3900
x = (3900-6y)/3
x + 2y – 1300 = 0 …(i)
And
x+3y = 1300
x = 1300 – 3y
x + 3y – 1300 = 0 …(ii)
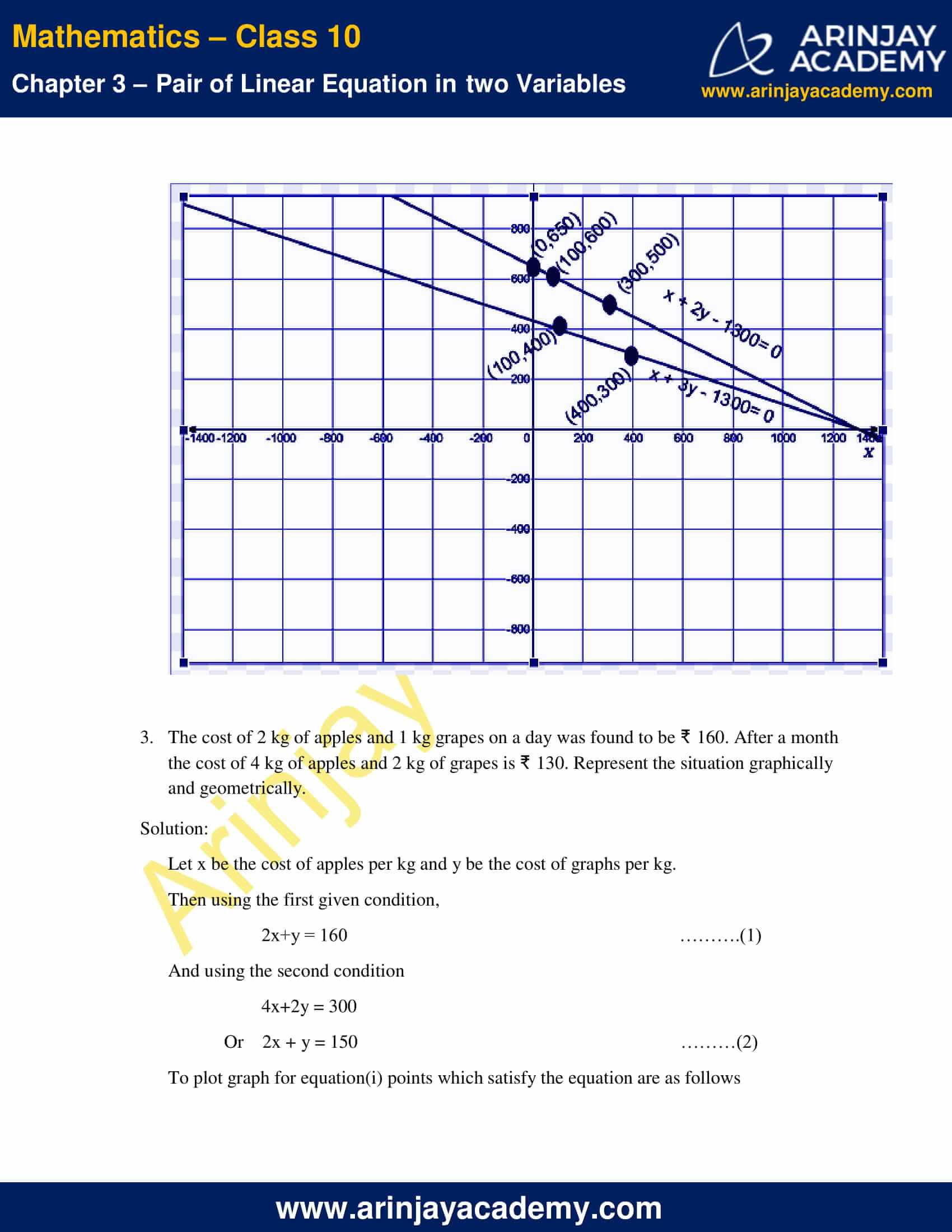
To plot graph for equation(i) points which satisfy the equation are as follows

To plot graph for equation(ii) points which satisfy the equation are as follows

Hence the graphical representation of equations (i) and (ii) is
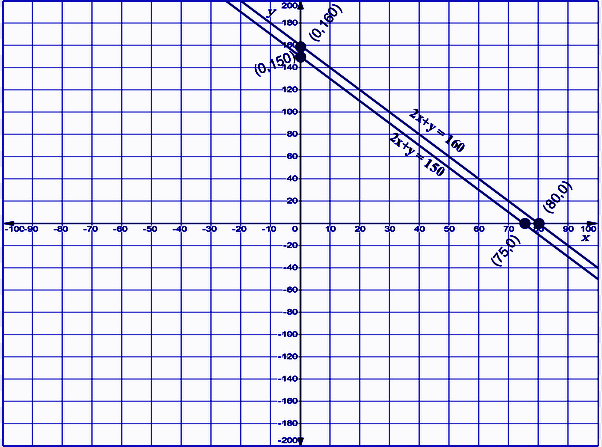
3. The cost of 2 kg of apples and 1 kg grapes on a day was found to be ₹ 160. After a month the cost of 4 kg of apples and 2 kg of grapes is ₹ 130. Represent the situation graphically and geometrically.
Solution:
Let x be the cost of apples per kg and y be the cost of graphs per kg.
Then using the first given condition,
2x+y = 160 ….(1)
And using the second condition
4x+2y = 300
Or 2x + y = 150 ……(2)
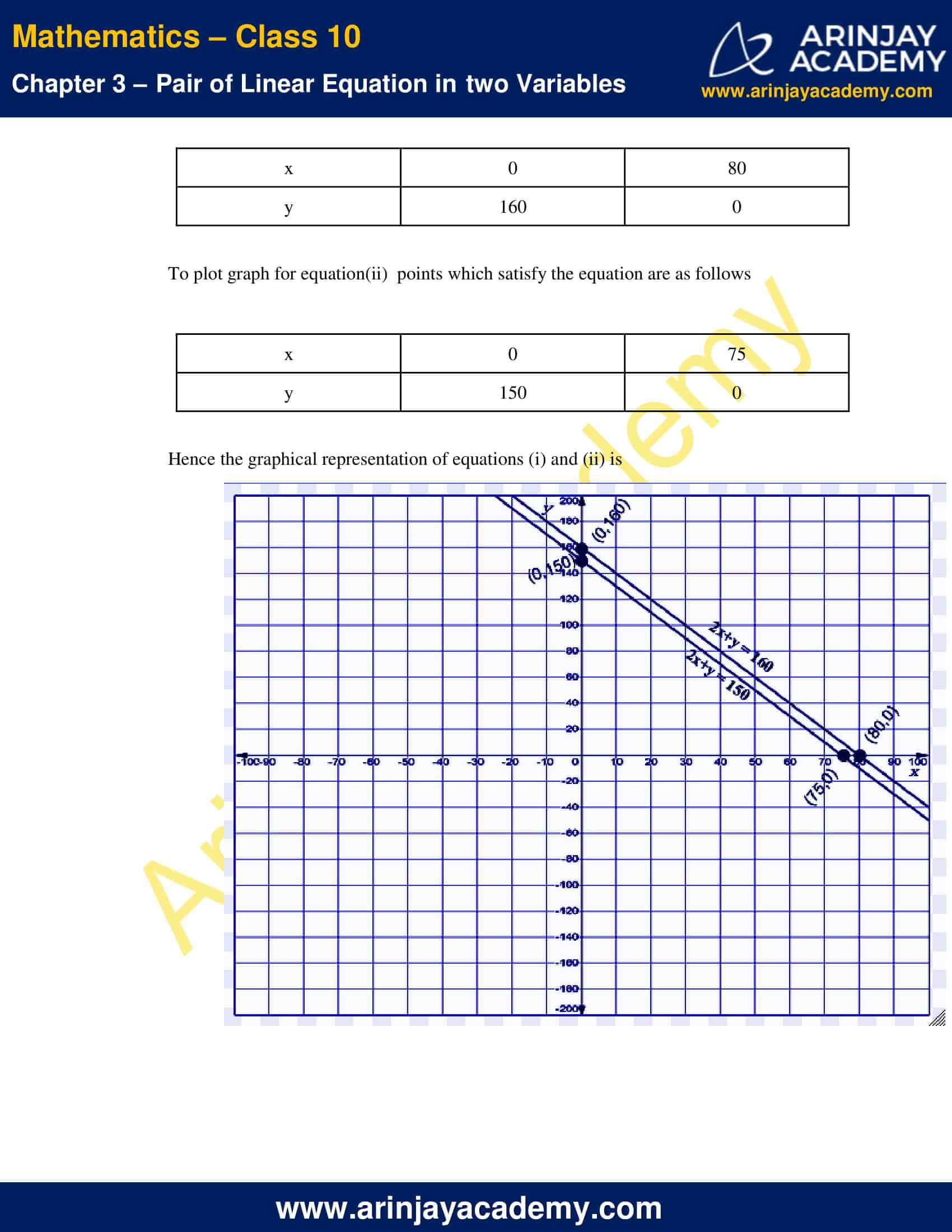
To plot graph for equation(i) points which satisfy the equation are as follows

To plot graph for equation(ii) points which satisfy the equation are as follows

Hence the graphical representation of equations (i) and (ii) is
NCERT Solutions for Class 10 Maths Chapter 3 Exercise 3.1 – Pair of Linear Equations in two Variables, has been designed by the NCERT to test the knowledge of the student on the topic – Pair of Linear Equations in Two Variables
