NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.3 – Polynomials contain 5 questions, for which detailed answers have been provided in this note.
| Category | NCERT Solutions for Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Exercise | Exercise 2.3 |
| Chapter Name | Polynomials |
Download NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.3 – Polynomials
NCERT Solutions For Class 10 Maths Chapter 2 Exercise 2.3 – Polynomials
1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2
Solution :
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
Applying long division as follows
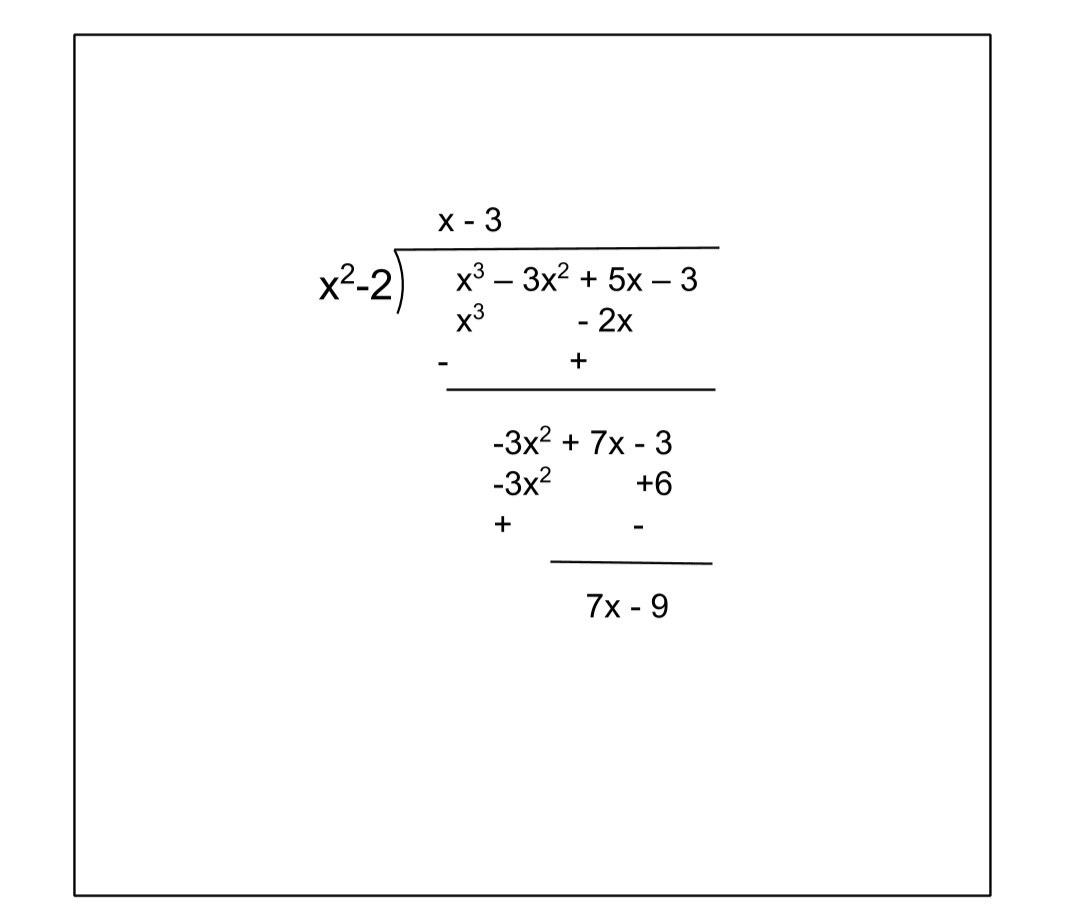
Therefore, we get
Quotient = x – 3 and Remainder = 7x – 9.
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x = x2 – x +1
Applying long division as follows
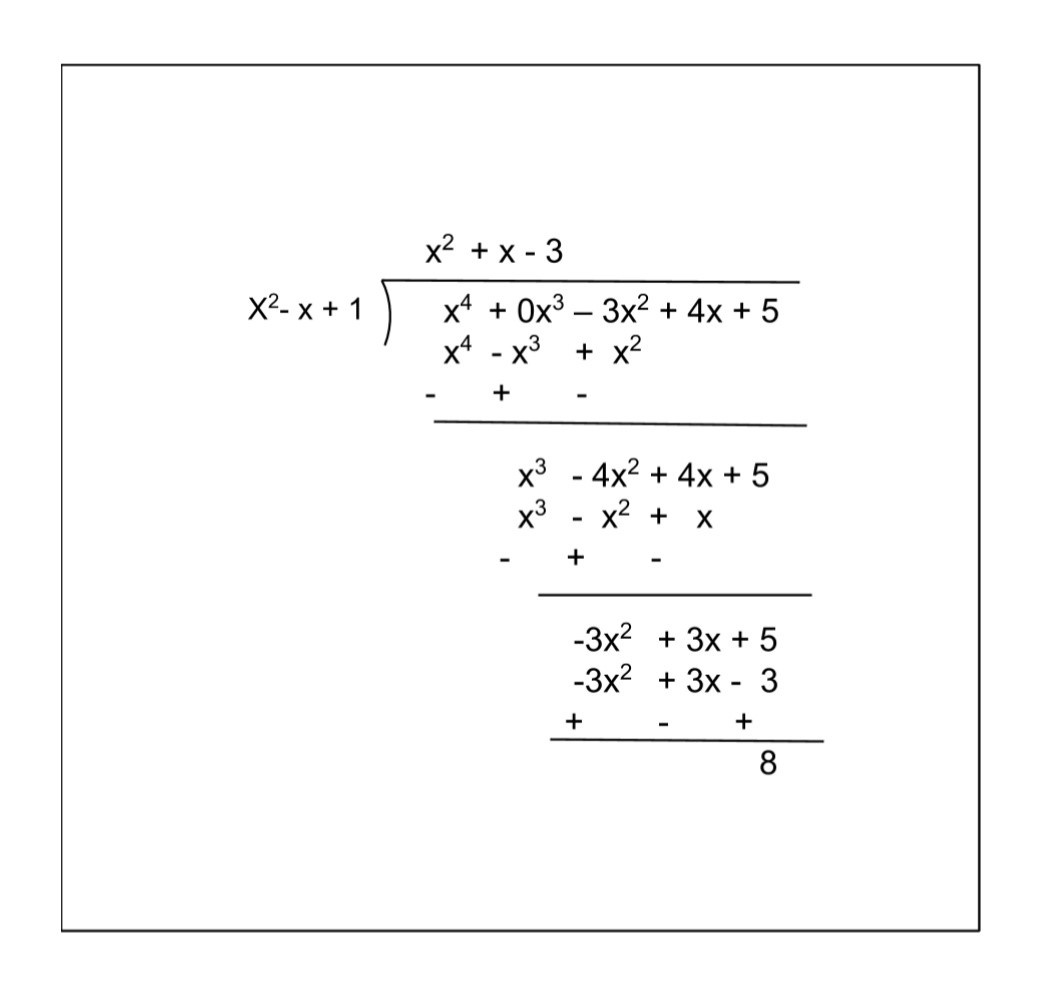
Therefore, we get
Quotient = x2 + x – 3 and Remainder = 8.
(iii) p(x) = x4 – 5x + 6 = x4 + 0x2– 5x + 6
g(x) = 2 – x2 = – x2 + 2
Applying long division as follows
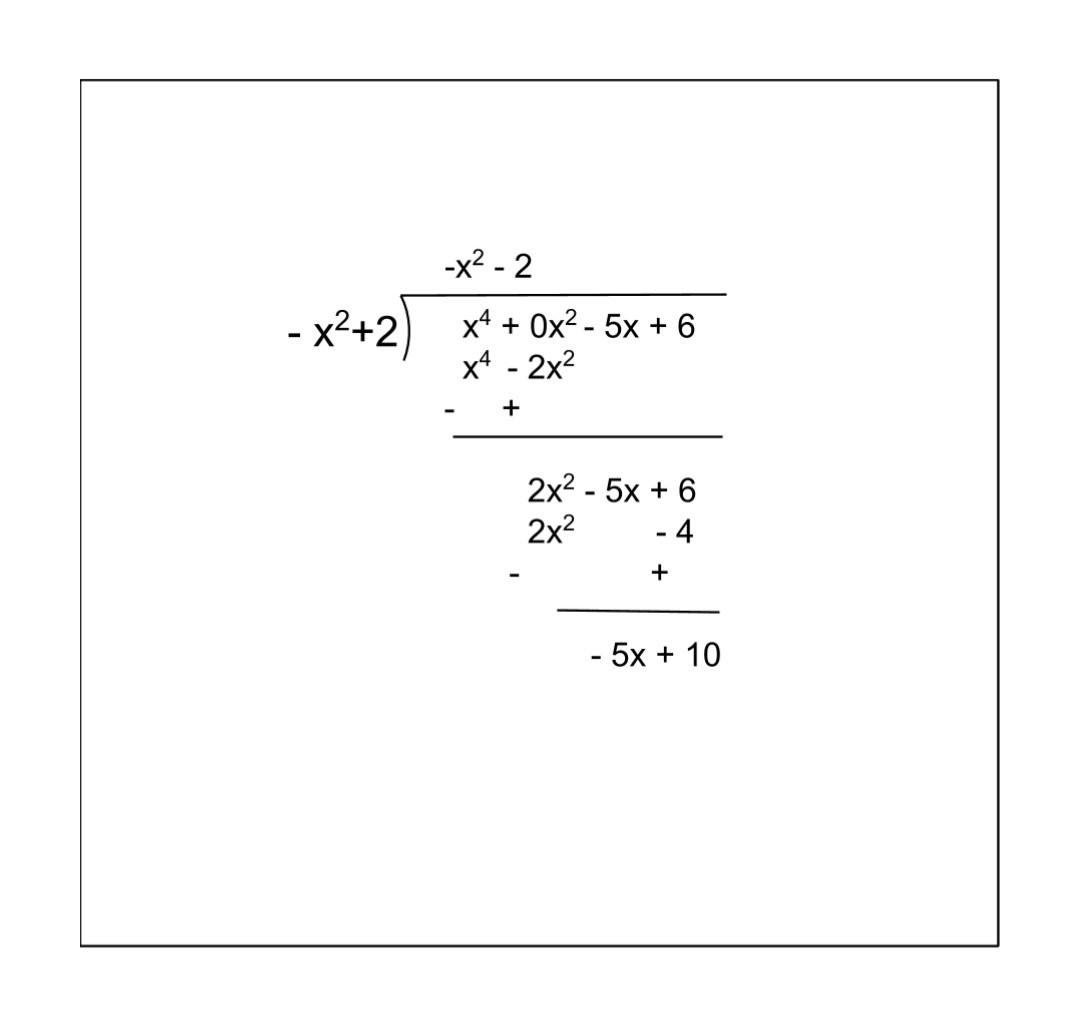
Therefore, we get
Quotient = -x2 – 2 and Remainder = -5x + 10.
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution :
(i) Applying long division as follows

Since we get, Remainder = 0, therefore the polynomial t2 – 3 is a factor of 2t4 + 3t3 – 2t2 – 9t – 12.
(ii) Applying long division as follows
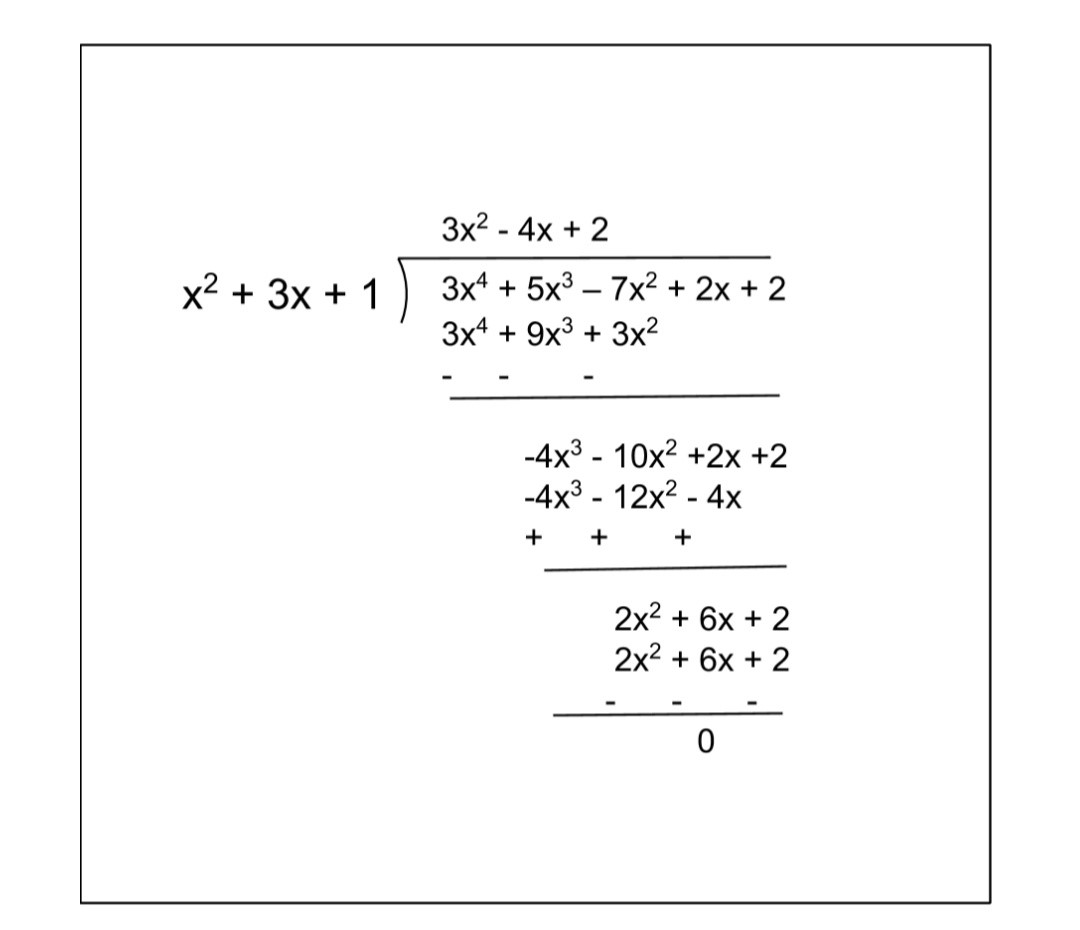
Since we get, Remainder = 0, therefore the polynomial x2 + 3x + 1 is a factor of 3x4 + 5x3 – 7x2 + 2x + 2.
(iii) Applying long division as follows

Since we get, Remainder = 2, therefore the polynomial x3 – 3x + 1 is not a factor of x5 – 4x3 + x2 + 3x + 1.
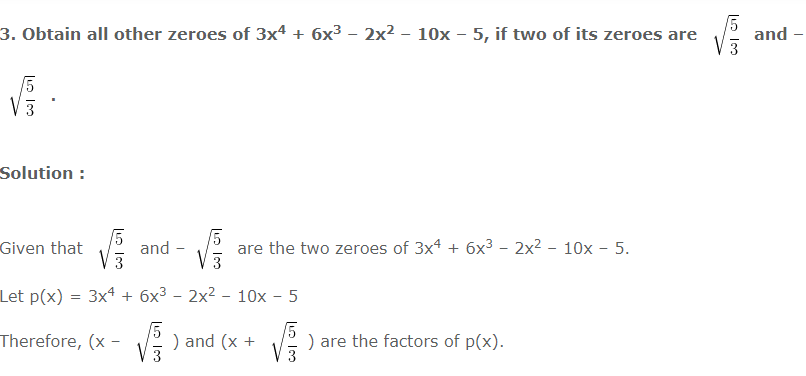
Hence, (x2 – (5/3)) is a factor of p(x).
For the other two factors applying long division as follows :

Thus,
3x4 + 6x3 – 2x2 – 10x – 5
= (x2 – (5/3)) (3x2 + 6x + 3)
= 3(x2 – (5/3)) (x2 + 2x + 1)
= 3(x2 – (5/3)) (x2 + x + x + 1)
= 3(x2 – (5/3)) (x(x+1) + 1(x + 1))
= 3(x2 – (5/3)) (x + 1)(x + 1)

4. On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4, respectively. Find g(x).
Solution :
Given
Divisor = g(x)
Quotient = x – 2
Dividend = x3 – 3x2 + x + 2
Remainder = -2x + 4
We know that,
Dividend = Divisor x Quotient + Remainder
Therefore,
x3 – 3x2 + x + 2 = g(x).(x – 2) + (-2x + 4)
g(x).(x – 2) = (x3 – 3x2 + x + 2) – (-2x + 4)
g(x).(x – 2) = (x3 – 3x2 + 3x – 2)
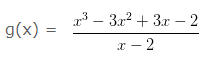
Applying long division as follows :

g(x) = x2 – x + 1
5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution :
According to the division algorithm p(x) = g(x)q(x) + r(x) , where q(x) , degree of r(x) = 0 or degree of r(x) < degree of g(x).
(i) deg p(x) = deg q(x)
p(x) = 2x2 + 4x + 3
q(x) = x2 + 2x + 1
g(x) = 2
r(x) = 1
the given condition is satisfied.
(ii) deg q(x) = deg r(x)
p(x) = x4 + x
q(x) = x
g(x) = x3
r(x) = x
the given condition is satisfied.
(iii) deg r(x) = 0
p(x) = 2x2 + 4x + 3
q(x) = x2 + 2x + 1
g(x) = 2
r(x) = 1
the given condition is satisfied.
NCERT Solutions for Class 10 Maths Chapter 2 Exercise 2.3 – Polynomials, has been designed by the NCERT to test the knowledge of the student on the topic – Division Algorithm for Polynomials