Mean, Median and Mode Questions, deals with various concepts which are as under:-
- Finding median when number of observation are Even
- Finding median when number of observation are Odd
- Finding Mean using frequency distribution table
- Finding unknown value when mean is given
- Finding the mode of given data
- Finding Mean, Median and Mode
- Finding the mean of ungrouped data
- Finding the median for frequency distribution (even terms)
- Finding the median for frequency distribution (odd terms)
- Finding the median of odd & even numbers
- Finding the mode value
Mean, Median and Mode Questions – Finding median when number of observation are Even
Question 1
The weights of 6 students (in kg) are 14, 26, 28, 20, 35, 30. Find the median weight ?
Explanation:
We would first arrange the given terms in ascending order
14, 20, 26, 28, 30, 35
Median = Median is the middle-most observation of the data.
In the present case N = 6, which is even .
Median weight for an even number of terms

= 27 kg
Hence, Median weight = 27 kg
Mean, Median and Mode Questions – Finding median when number of observation are Odd
Question 2
The runs scored by 9 players of a cricket team are 44, 31, 50, 40, 50, 70, 11, 80, 56 Find the median score ?
Explanation:
We would first arrange the given terms in ascending order
11, 31, 40, 44, 50, 50, 56, 70, 80
Median = Median is the middle-most observation of the data.

= Value of 5 th term
Hence, the runs for an odd number of terms = 50
Mean, Median and Mode Questions – Finding Mean using frequency distribution table
Question 3
Given table shows the height of 12 boys . Find the mean Height ?

Explanation:
For calculating the mean, we need to prepare a table :
To find the mean using frequency Distribution, we would need to follow the following steps : –
Let the Height be represented by xi
Let the Number of boys be represented by ƒi
For each value, we would find the product of xi and ƒi
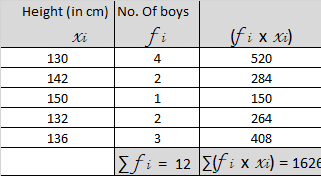
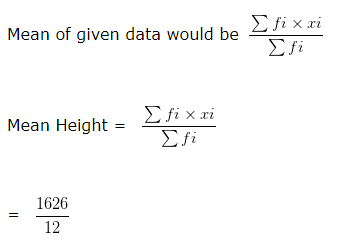
= 135.5 cm
Hence, the Mean Height is 135.5 cm
Mean, Median and Mode Questions – Finding unknown value when mean is given
Question 4
If the mean of the given frequency distribution is 6 , find the value of p ?

Explanation:
For calculating the mean, we need to prepare the following table :

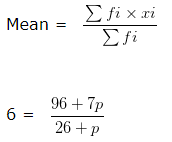
6 x ( 26 + p ) = 96 + 7
156 + 6p = 96 + 7p
156 – 96 = 7p – 6p
60 = 1p
p = 60/1
p = 60
Mean, Median and Mode Questions – Finding the mode of given data
Question 5
Find the modal value of the given data :

Explanation:
Mode = Mode is the value which occurs the most frequently.
Since the number of boys of age group 15 is maximum .
So, the modal age of boys is 15 .
Mean, Median and Mode Questions – Finding Mean, Median and Mode
Question 6
Find the mean and median for the given data, using empirical formula. Also calculate its mode ?

Explanation:
Distribution table for the given data would be as under:
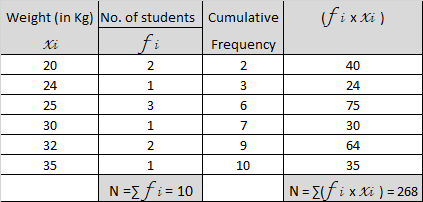

= 1/2 [ 25 + 25 ] Cumulative frequency shows that value of 5th term and 6th term is 25
= 1/2 x 50
Median = 25 kg
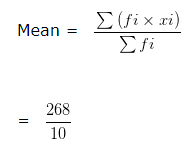
= 26.8 kg
Mode = 3( Median ) – 2( Mean )
= 3 x 25 – 2 x 26.8
= 75 – 53.6
= 21.4 kg
Hence, Median = 25 kg , Mean = 26.8 kg , Mode = 21.4 kg .
Mean, Median and Mode Questions – Finding the mean of ungrouped data
Question 7
Find the mean of the data given below . 10, 5, 13, 4, 9, 12, 11 and 24
Explanation:
Mean is the Average of given data
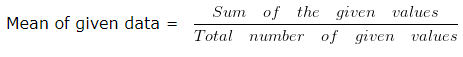
Sum of given data = 10 + 5 + 13 + 4 + 9 + 12 + 11 + 24
Sum of given data = 88
Total number of values = 8
Mean of given data = 88/8
Mean of given data = 11
Mean, Median and Mode Questions – Finding the median for frequency distribution (even terms)
Question 8
Find the median for the given frequency distribution :

Explanation:
We would first arrange the given terms in ascending order

To find the median, we would prepare the cumulative frequency table, and find the middle observation of given set
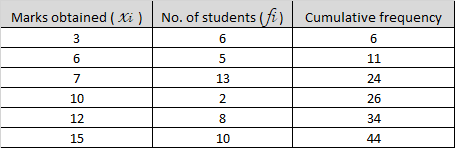
Total number of terms, N = 44
Median = Median is the middle-most observation of the data.
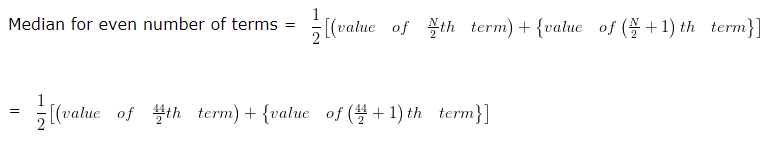
= 1/2 [ value of 22nd term + value of 23rd term ]
= 1/2 [ 7 + 7 ] Since, cumulative frequency shows the value of each one of 22nd and 23rd term is 10
= 1/2 x 14
= 7
Hence, Median for even number of terms = 7
Mean, Median and Mode Questions – Finding the median for frequency distribution (odd terms)
Question 9
Find the median for the given frequency distribution :

Explanation:
We would first arrange the given terms in ascending order

To find the median, we would prepare the cumulative frequency table, and find the middle observation of given set
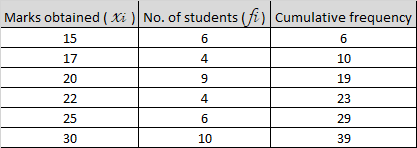
Total number of terms = 39 , which is odd.
Median = Median is the middle-most observation of the data.

= 20 th student
Since, Cumulative frequency shows that 20 th student gets 22 marks .
Hence, median marks = 22
Mean, Median and Mode Questions – Finding the median of odd & even numbers
Question 10
Find the median of odd numbers between 8 and 25 ?
Explanation:
Odd numbers between 8 and 25 are
9 , 11 , 13 , 15 , 17 , 19 , 21 , 23
Here, N = 8 , which is even
Median = Median is the middle-most observation of the data.
Median of even number of terms

= 18
Hence, median of odd numbers between 8 and 25 is 18
Mean, Median and Mode Questions – Finding the mode value
Question 11
Find the mode of the given data : 14, 12, 4, 14, 2, 12, 14, 3, 2, 10
Explanation:
We would first arrange the given marks in ascending order,
2 , 2 , 3 , 4 , 10 , 12 , 12 , 14 , 14 , 14
Mode of the given data is the value which occurs the most frequently.
The terms and the frequency are given as under
Term = Frequency
2 = 2
3 = 1
4 = 1
10 = 1
12 = 2
14 = 3
Since, 14 occurs maximum number of times.
Hence, mode = 14