Lines and Angles Class 9 MCQ with Answers – Maths Class 9 MCQ Online Test are covered in this Article. Lines and Angles Class 9 MCQ Test contains 30 questions. Answers to MCQ on Lines and Angles Class 9 are available after clicking on the answer. MCQ Questions for Class 9 with Answers have been made for Class 9 students to help check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Board | CBSE |
| Textbook | Maths (NCERT) |
| Class | Class 9 |
| Chapter | Chapter 6 Lines and Angles |
| Category | MCQ Questions for Class 9 Maths with Answers |
Lines and Angles Class 9 MCQ with Answers
1. If three or more points lie on the same line, they are called
(a)collinear
(b)non-collinear
(c)either (a) or (b)
(d)neither (a) and (b)
Answer
Answer: (a)collinear
2. Two angles whose sum is 90° are called
(a)acute angle
(b)right angle
(c)supplementary angle
(d)complementary angle
Answer
Answer: (d)complementary angle
3.In figure which of the following angles are vertically opposite
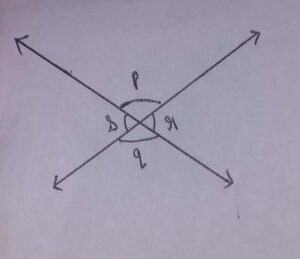
(a)∠p and ∠s
(b) ∠s and ∠q
(c) ∠r and ∠p
(d) ∠p and ∠q
Answer
Answer: (d) ∠p and ∠q
4.Two parallel lines intersect at
(a)1 point
(b)2points
(c)no point
(d)4 points
Answer
Answer: (c)no point
5. If ∠MOX = 90°, and ∠NOY = 67°, then ∠MON =
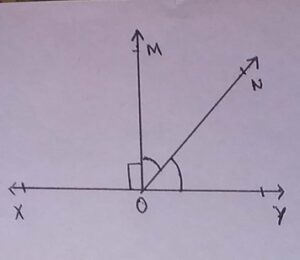
(a)23°
(b)27°
(c)33°
(d)37°
Answer
Answer: (a)23°
Explanation: ∠MOX +∠NOY +∠MON = 180° [Linear pair of angles]
By putting values
90° + 67° + ∠MON = 180°
157° + ∠MON = 180°
∠MON=180° -157°
∠MON = 23°
6.The sum of the three angles of a triangle is
(a)180°
(b) 80°
(c) 170°
(d) 160°
Answer
Answer: (a)180°
7. If ∠AQP = 110° and ∠BRP = 125°, then ∠QPR is

(a)45°
(b)55°
(c)65°
(d)75°
Answer
Answer: (b)55°
Explanation: ∠AQP + ∠PQR = 180° [ Linear pair of angles]
110° + ∠PQR = 180°
∠PQR = 70°
∠PRB +∠PRQ = 180° [ Linear pair of angles]
125° + ∠PRQ = 180°
∠PRQ = 55°
Now, In triangle PQR
∠PRQ + ∠PQR + ∠QPR = 180°
55° + 70° + ∠QPR = 180°
∠QPR = 180° -125°
∠QPR=55°
8. If a + b + f = d + e + c, then POQ is
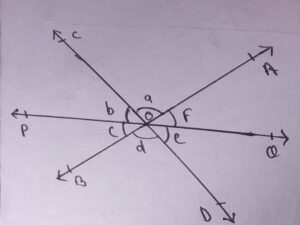
(a)Line
(b)Triangle
(c)either line and triangle
(d)none of these
Answer
Answer: (a)Line
Explanation: Given, a + b + f = d + e + c
We know that the angles around a point are 360° so,
a + b + f + d + e + c = 360°
2 (a + b + f) = 360°
a + b + f = 180°
Hence, POQ is a line.
9. A line joining two end points is called
(a)ray
(b) line segment
(c)parallel line
(d) None of these
Answer
Answer: (b) line segment
10. Consecutive interior angles of the transversal are
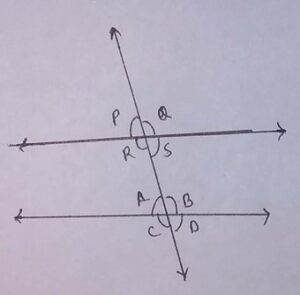
(a)∠P and ∠A
(b) ∠P and ∠C
(c) ∠S and ∠B
(d) ∠S and ∠A
Answer
Answer: (c) ∠S and ∠B
Lines and Angles Class 9 MCQ with Answers
11. If a transversal intersects two parallel lines, then each pair of corresponding angles are
(a)equal
(b)unequal
(c)double
(d)half
Answer
Answer: (a)equal
12.MN is a transversal which intersects two parallel lines PQ and RS and ∠A=70°,∠B,∠C and ∠D are interior angles, then ∠C =
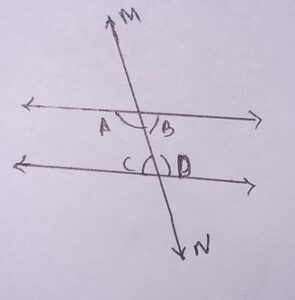
(a)90°
(b)110°
(c)180°
(d)360°
Answer
Answer: (b)110°
Explanation: We know that, if a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
∠A+∠C = 180°
∠C= 180° – 70°
∠C=110°
13. A line with one end point is called a
(a)ray
(b)line segment
(c)either ray or line
(d)None of these
Answer
Answer: (a)ray
Explanation:
14. AB || CD and EF⊥ AB, ∠EGH = 55°, then what will be the value of x, y, w and z
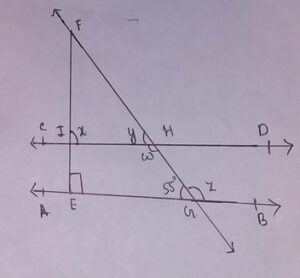
(a)x = 90°, y = 55°, w = z = 125°
(b) x = y = 55°, w = z = 125°
(c)x = 55°, y = 45°, w = z = 125°
(d) x = 90°, y = w = z = 125°
Answer
Answer: (a)x = 90°, y = 55°, w = z = 125°
Explanation: ∠GEF =x [Corresponding angles]
x = 90°
Now,
∠EGH = 55°
w + ∠EGH = 180° [pair of interior angles on the same side of the transversal is supplementary]
w + 55° = 180°
w = 125°
Now, y = ∠EGH [Corresponding angles]
y = 55°
Now, w = z [Alternate interior angles]
z = 125°
15. In below figure, find ∠S and ∠T
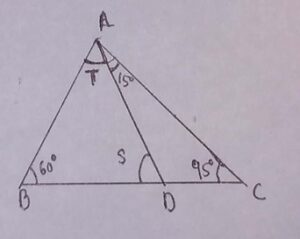
(a) ∠S = 10°, ∠T = 110°
(b) ∠S = 110°, ∠T = 100°
(c) ∠S = 110°, ∠T = 10°
(d) ∠S = 120°, ∠T = 10°
Answer
Answer: (c) ∠S = 110°, ∠T = 10°
Explanation: In triangle ADC
∠ADB = ∠DAC + ∠ACD [If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.]
∠ADB = ∠S = 15° + 95°
∠S = 110°
Now, In triangle ADB
∠S+∠T+∠ABD = 180° [Angle sum property]
110° + ∠T + 60° = 180°
∠T = 180° – 170°
∠T = 10°
16. AD ⊥ PQ and BC ⊥ PQ, then find value of x

(a) x = 10°
(b) x = 60°
(c) x = 70°
(d) x = 80°
Answer
Answer: (a) x = 10°
Explanation: In triangle ADC
∠ADC + ∠ACD +∠DAC = 180° [angle sum property]
80° + 90° +∠DAC = 180°
∠DAC = 180° – 170°
∠DAC = y = 10°
Now, y + ∠BAC = 90° [AD ⊥ PQ]
10° + ∠BAC = 90°
∠BAC = 90° – 10°
∠BAC = 80°
Now, In triangle ABC
∠BAC + ∠ABC + x = 180° [angle sum property]
80° + 90° + x = 180°
x = 10°
17: The value of a straight angle is
(a)180°
(b) 90°
(c)0°
(d)None of these
Answer
Answer: (a)180°
18 In the below figure, find value of x
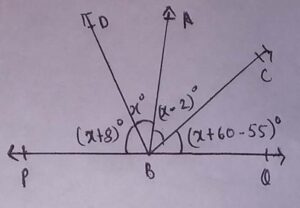
(a) 40(1/4)°
(b) 42(4/1)°
(c) 41(1/4)°
(d) 42(1/4)°
Answer
Answer: (d) 42(1/4)°
Explanation: ∠x+8° + ∠x + ∠x – 2° + ∠x + 60° -55° = 180° [Linear pair of angles]
4∠x + 11° = 180°
4∠x = 169°
∠x = 169/4 = 42(1/4)°
19.If lines PT and SQ intersect at point R, such that ∠ PRQ = 60°, ∠ RTS = 50°, find ∠ RST

(a) 60°
(b) 50°
(c) 70°
(d) 80°
Answer
Answer: (c) 70°
Explanation: PT and SQ intersect at point R
∠ PRQ = ∠ SRT =60° [Vertically opposite angle]
In triangle SRT
∠ SRT +∠ RST + ∠ RTS = 180 [ Angle sum property]
60° + ∠ RST + 50° = 180°
∠ RST = 180° – 110°
∠ RST = 70°
Lines and Angles Class 9 MCQ with Answers
20 If one angle of triangle is equal to the sum of the other two, then the triangle is
(a) an isosceles triangle
(b) an obtuse-angled triangle
(c) an equilateral triangle
(d) a right triangle
Answer
Answer: (d) a right triangle
Explanation: The sum of interior angles of a triangle is equal to 180°. In the right triangle, one angle should be equal to 90°, and the remaining two angles are acute angles, and their sum is equal to 90°.
21. If lines AE and BD intersect at point C, ray CF is the angle bisector of ∠ACB and ∠AFC=∠BCF = 90°, ∠CED = 100° and ∠DCE = 50°, then
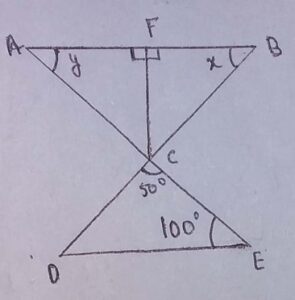
(a) x <y
(b) x = y
(c) x >y
(d) x ≠ y
Answer
Answer: (b) x = y
Explanation: Lines AE and BD intersect at point C
∠DCE = ∠ACB = 50° [Vertically opposite angle]
CF is the angle bisector of ∠ACB
So, ∠ACF = ∠BCF = 1/2×∠ACB
∠ACF = ∠BCF = 1/2×50° = 25°
Now, In triangle ACF
∠ACF+ ∠AFC + y = 180° [angle sum property]
25° + 90° + y = 180°
y = 180° – 115°
y =65° ………… (1)
Similarly, In triangle BCF
∠BCF+ ∠BFC + x = 180° [angle sum property]
25° + 90° + x = 180°
x = 180° – 115°
x =65°………………. (2)
From (1) and (2)
x =y =65°
22. If ratio of angles of a triangle is 3:4:5 then the value of largest angle is
(a) 75°
(b) 85°
(c) 95°
(d) 105°
Answer
Answer: (a) 75°
Explanation: Let the angles of the triangle be 3x, 4x and 5x.
Now, 3x + 4x + 5x = 180° [angle sum property]
12x = 180°
x = 180°/12
x = 15°
Now, the angles of the triangle are 3×15° = 45°
4×15° = 60°
5 ×15°= 75°
23. The triangle whose angles are in the ratio 7:3:5, is called
(a)an acute angled triangle
(b) an obtuse-angled triangle
(c) an equilateral triangle
(d) a right triangle
Answer
Answer: (a)an acute angled triangle
Explanation: Let the angles of the triangle be 7y, 3y and 5y.
Now, 7y + 3y + 5y = 180° [angle sum property]
15y = 180°
y = 12°
The angles of the triangle are 84°, 36°, 60°.
So, value of all angles is less than 90°, the triangle is acute angled triangle.
24. If PQ || RS, AB ⊥ PQ and ∠ ACS = 131°, find ∠BAC

(a) ∠BAC = 21°
(b) ∠BAC = 31°
(c) ∠BAC = 41°
(d) ∠BAC = 51°
Answer
Answer: (c) ∠BAC = 41°
Explanation: ∠BAC + ∠PAB = 131° [alternate interior angle]
∠BAC + 90° = 131°
∠BAC = 131°-90°
∠BAC = 41°
25. A reflex angle is:
(a)more than 90°
(b)less than 180°
(c)more than 180°
(d)less than 90°
Answer
Answer: (c)more than 180°
26. If the angles a and b are in the ratio 5: 6, then angle c is
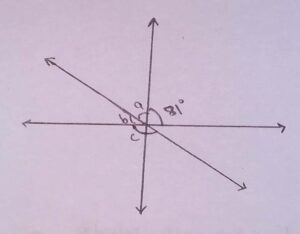
(a) ∠c = 66°
(b) ∠c = 106°
(c)∠c = 116°
(d) ∠c = 126°
Answer
Answer: (d) ∠c = 126°
Explanation: Let the angles a and b are 5x and 6x.
∠a +∠b + 81° = 180° [linear pair of angles]
5x + 6x = 180° – 81°
11x = 99°
x = 9°
∠a = 5x = 5(9°) = 45°
∠b = 6x = 6(9°) = 54°
∠c +54° = 180° [linear pair of angles]
∠c = 180° – 54°
∠c = 126°
27. The diagonals of a square ABDC intersect at O. If ∠ABO = 61°, then ∠OAB is:
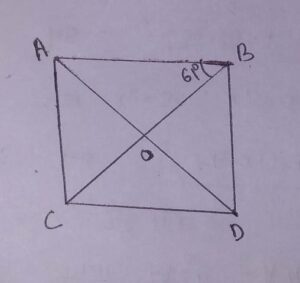
(a) 28°
(b) 29°
(c) 30°
(d) 31°
Answer
Answer: (b) 29°
Explanation: We know that diagonals of a square bisect each other at right angles.
So, ∠AOB = 90°
Now, In triangle ABO
∠AOB + ∠ABO+∠OAB = 180° [angle sum property]
90° + 61° + ∠OAB = 180°
∠OAB = 180° – 151°
∠OAB = 29°
28. If ratio of two supplementary angles is 2x:3x, then the angles are
(a)72°, 108°
(b)110°, 70°
(c)60°,120°
(d)100°, 80°
Answer
Answer: (a)72°, 108°
Explanation: We know that supplementary angles are those angles whose sum is 180°.
2x + 3x = 180°
5x = 180°
x = 36°
Two angles are 72° and 108°.
29. The value of an obtuse angle is
(a)less than 90°
(b) less than 180°
(c) less than 270°
(d) greater than 90° and less than 180°
Answer
Answer: (d) greater than 90° and less than 180°
30. The value of each angle of an equilateral triangle is
(a)70°
(b)65°
(c)60°
(d)55°
Answer
Answer: (c)60°
Explanation: We know that the angles of an equilateral triangle is in the ratio 1:1:1.
Let angles be x, x and x
x +x + x = 180° [angle sum property]
3x = 180°
x = 60°
MCQ Questions for Class 9 Maths
- Number Systems Class 9 MCQ with Answers
- Polynomials Class 9 MCQ with Answers
- Coordinate Geometry Class 9 MCQ Questions
- Linear Equations in Two Variables Class 9 MCQ with Answers
- Lines and Angles Class 9 MCQ with Answers
- Triangles Class 9 MCQ with Answers
- Quadrilaterals Class 9 MCQ Questions
- Circles Class 9 MCQ with Answers
- Constructions Class 9 MCQ
- Heron’s Formula Class 9 MCQ with Answers
- Surface Area and Volume Class 9 MCQ
- Statistics Class 9 MCQ
- Probability Class 9 MCQ with Answers
Frequently Asked Questions on Lines and Angles Class 9 MCQ with Answers
1. Are these MCQ on Lines and Angles Class 9 are based on 2021-22 CBSE Syllabus?
Yes. There are 30 MCQ’s on this Chapter in this blog.
2. Are you giving all the chapters of Maths Class 9 MCQs with Answers which are given in CBSE syllabus for 2021-22 ?
Yes, we are providing all the chapters of Maths Class 9 MCQs with Answers.