Large Numbers Class 4

Large Numbers Class 4, deals with various concepts which are as under:-

• Successor in Maths
• Predecessor in Maths
• Consecutive Numbers
• Place value
• Expanded Form
• Standard form
• Rounding off numbers
• Roman Numerals

Large Numbers Class 4 – Successor in Maths

Successor of any whole number,  is the number, obtained by adding 1 to that number.

Question 1

Find the successor of 22820?

Explanation:

The “Successor” of any whole number is the number, obtained by adding 1 to that number.

So, the successor of 22820 is 22820 + 1 = 22821

 

Large Numbers Class 4 – Predecessor in Maths

Predecessor of any whole number is the number obtained by subtracting 1 from it.

Question 2

Find the predecessor of 26333?

Explanation:

The “Predecessor” of any whole number is the number obtained by subtracting 1 from it.
So, the predecessor of 26333 is 26333 – 1 = 26332

Large Numbers Class 4 – Consecutive Numbers

Consecutive numbers are numbers,  that follow each other , in the order of smallest to largest.

In other words, we can say that consecutive number of any given number is obtained by adding 1 to that number.

Question 3

Write the three consecutive numbers occurring just after 36135.

Explanation:

The next three consecutive number of 36135 can be obtained by adding 1, 2 and 3 to 36135
that is,
36135 + 1 = 36136
36135 + 2 = 36137
36135 + 3 = 36138

Hence the three consecutive number occurring just after 36135 are 36136, 36137 and 36138 respectively.

 

Large Numbers Class 4 – Place value

Place value of the digit , is the value of  digit in a given number , with reference to its position in a given  number. It is obtained as a  Product of the digit , and the value of its place in the digit (ones, tens, hundreds, thousandth).

Question 4

Place value of 2 in 982764 is?

Explanation:

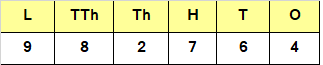
2 is in thousands place.

Thus, the place value of 2 is 2 x 1000 = 2000

 

Large Numbers Class 4 – Expanded Form

In order to find Expanded form of a number, we write the value of each of the digits in the number, according to its place value and express it as a sum of all these values. The steps involved are as under : –

• Step – 1 – Write the value of each of the digits in the number, according to its place value
• Step – 2 – Express the number, as the  sum of all these values.

In other words, we can say that writing a number as the sum of the place value of the digits.

Question 5

Write expanded form of 54328?

Explanation:

In expanded form , we write the value of each of the digits, according to its place value
In 54328
5 is in ten thousands place.
5 x 10000 = 50000
4 is in thousands place.
4 x 1000 = 4000
3 is in hundreds place.
3 x 100 = 300
2 is in tens place.
2 x 10 = 20
8 is in ones place
8 x 1 = 8
If we add above results, we would get
50000 + 4000 + 300 + 20 + 8

Large Numbers Class 4 – Standard form

Standard form of a number is obtained by combining , the face value of each digit.

Question 6

Write the standard form of 300000 +20000 + 4000 + 600 + 70 + 2

Explanation:

In order to get the standard form of a given number, we have to divide them by their place values

For Lakhs place 300000 ÷ 100000 = 3

For Ten thousands place 20000 ÷ 10000 = 2

For Thousands place: 4000 ÷ 1000 = 4

For Hundreds Place: 600 ÷ 100 = 6

For Tens Place: 70 ÷ 10 = 7

For Units Place: 2 ÷ 1 = 2

Hence, the standard form of the given number is 324672

 

Large Numbers Class 4 – Rounding off numbers

Rounding off numbers to the nearest 10 ( Tens ).

• For rounding off a given number to the nearest tens. we will first check if the ones digit is greater than or lesser than 5.
• If the one’s digit is greater than 5, we will increase tens digit by 1, and replace ones digit by 0.
• If one’s digit is lesser than 5, we will replace ones digit by 0, and other digits remain same.

Question 7

Round off the given digit to the nearest ten.
49

Explanation:

In, present case,
49 has the number 9 in ones place
Since,
9 > 5
Hence, the required rounded number = 50

 

Rounding off numbers to the nearest 100 ( Hundreds )

• In order to round off a given number to the nearest hundreds we will first check if the tens digit is greater than or lesser than 5
• If the ten’s digit is greater than 5, we will increase hundreds digit by 1 and replace tens or ones digit by 0. 
• If the ten’s digit is lesser than 5, we will replace tens or ones digit by 0, and other digits remain same. 

Question 8

Round off the given number to the nearest hundred.
427

Explanation:

In, present case,
We have 427 in which 2 is in tens place and 7 in ones place
We know that 2 < 5
Hence, the required rounded number is 400

Rounding off numbers to the nearest 1000 ( Thousands ).

• In order to round off a given number to the nearest thousands we will first check if the hundreds digit is greater than or lesser than 5
• If the hundred’s digit is greater than 5, we will increase thousands digit by 1 and replace hundreds, tens and ones digit by 0. 
• If the hundred’s digit is lesser than 5, we will replace hundreds, tens and ones digits by 0, and other digits remain same.

Question 9

Round off the given number to the nearest thousand.
3846

Explanation:

In, present case,
We have 3846 in which 8 is in hundred place , 4 is in tens place and 6 in ones place
So, 8 > 5
Hence, the required estimated number is 4000

Large Numbers Class 4 – Roman Numerals

Rule 1 – Repetition of a Roman Numeral means addition.

• Only letters I, X, C, M can be repeated.
• No letter can be repeated more than 3 times.
• Letter V, L, D are never repeated.

Rule 2 – When a smaller numeral is placed on the left of the larger numeral, it means Subtraction.

• I can be subtracted from V and X only.
• X can be subtracted from L and C only.
• C can be subtracted from D and M only.

Conversion of Hindu Arabic Numerals to Roman Numerals.

Question 10

Express 4 in Roman Numeral.

Explanation:

Step I : Express the number in expanded form.
4 = 5 – 1

Step II : Convert Expanded form of number in Roman Numeral.
5 – 1 = (V) – (I) = IV

Hence, 4 would be represented as IV in Roman Numeral.

Question 11

Express 48 in Roman Numeral.

Explanation:

Step I : Express the number in Expanded form.
48   =      40    +    5      +   3
= (50 – 10) +   5      +   3

Step II : Convert Expanded form of number in Roman Numeral.
(50 – 10) + 5 + 3 = (L – X) + (V) + (III)= XLVIII

Hence, 48 would be represented as XLVIII in Roman Numeral.

Conversion of Roman Numerals to Hindu Arabic Numerals.

Question 12

Express XVII in Hindu Arabic Numeral.

Explanation:

XVII = X + V + I + I
= 10 + 5 + 1 + 1
= 17

Hence, Roman Numeral XVII can be represented as 17 in Hindu Arabic Numeral.

Question 13

Express XIV in Hindu Arabic Numeral.

Explanation:

XIV = X + IV
= 10 + 4
= 14

Hence, Roman Numeral XIV can be represented as 14 in Hindu Arabic Numeral.

Click here for Class 4 Chapterwise Explanations