| Subject | Maths |
| Class | Class 7 |
| Category | Maths Class 7 |
| Topic | Angle Sum Property of a Triangle |
Proof of Angle Sum Property of a Triangle
Theorem – The sum of the angles of a triangle is 180˚
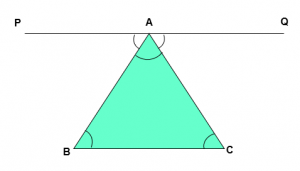
Proof – Consider a ∆ ABC
Draw a line PQ parallel to BC
∠PAB + ∠BAC + ∠ CAQ = 180˚ [Angle on straight line is equal to 180˚ ] — 1
Now BC || PQ and transversal AB cuts BC at B and PQ at A
∠PAB = ∠ABC [Alternate angles ] — 2
BC || PQ and transversal AC cuts BC at C and PQ at A
∠CAQ = ∠ACB [Alternate angles] — 3
From Equation 1, 2 and 3 we get,
∠ABC + ∠BAC + ∠ACB = 180˚
Hence, the sum of the angles of a triangle is 180˚.
Angle Sum Property of a Triangle Class 7 Examples –
Example 1
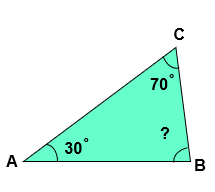
In the given triangle ABC, ∠BAC = 30˚, ∠ACB = 70˚, find the measure of ∠ABC ?
EXPLANATION
Given:
∠BAC = 30˚
∠ACB = 70˚
∠ABC = ?
According to Angle Sum Property of a triangle
∠BAC + ∠ACB +∠ABC = 180˚
30˚ + 70˚ + ∠ABC = 180˚
100˚ + ∠ABC = 180˚
∠ABC = 180˚ – 100˚
∠ABC = 80˚
Hence, the measure of ∠ABC is 80˚
Example 2
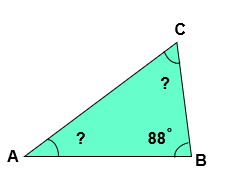
In the given triangle ABC, ∠ABC = 88 and ∠ACB = ∠BAC , then find the measure of ∠ACB and ∠BAC ?
EXPLANATION
Given:
∠ABC = 88˚
∠ACB = ?
∠BAC = ?
Let ∠ACB = ∠BAC = a
According to Angle Sum Property of a triangle
∠ABC + ∠ACB +∠BAC = 180˚
88˚ + a + a = 180˚
88˚ + 2a = 180˚
2a = 180˚ – 88˚
a = 92⁄2
a = 46˚
Hence, ∠ACB = ∠BAC = a = 46˚
Angle Sum Property of a Triangle Class 7 – Example 3
Find the angles of a triangle which are in the ratio 7 : 2 : 3
EXPLANATION
Let the measures of the given angles be:
1st angle = ( 7a )˚
2nd angle = ( 2a )˚
3rd angle = ( 3a )˚
Then, According to angle sum property of a triangle
1st angle + 2nd angle + 3rd angle = 180 ˚
7a + 2a + 3a = 180
12a = 180
a = 180⁄12
a = 15
So, 1st angle = ( 7a )˚ = ( 7 x a )˚ = ( 7 x 15 )˚ = 105˚
2nd angle = ( 2a )˚ = ( 2 x a )˚ = ( 2 x 15 )˚ = 30˚
3rd angle = ( 3a )˚ = ( 3 x a )˚ = ( 3 x 15 )˚ = 45˚
Hence, the measures of the angles of the triangle are 105˚ , 30˚ and 45˚