Ratio and Proportion Examples With Answers, deals with various concepts which are as under:-
- Converting Ratios to Simplest Form
- Equivalent Ratios
- Find the numbers when their ratio and sum are given
- Divide sum of money between two persons when ratio are given
- Divide sum of money among 3 persons when ratio are given
- Are the given number are in proportion
- Find the value of y when four numbers are in proportion
Ratio and Proportion Examples With Answers – Convert Ratio into its simplest form
In order to convert the given ratio to Simplest Form, we should follow the following steps : –
- Find the HCF of both the numerator and denominator
- Dividing Both numbers by their HCF
The result is the ratio in its simplest form.
Example 1
Convert the ratio 60 : 35 in its simplest form.
Solution
HCF of 60 and 35 is 5
Since, 60 : 35

= 12 : 7
Hence, the simplest form of 60 : 35 is 12 : 7
Ratio and Proportion Examples With Answers – Equivalent ratios
In order to find Equivalent Ratios of any given ratio, we multiply or divide the numerator and denominator of the ratio by the same non zero number.
Example 2
Find the Equivalent ratio of 2 : 3
8/9, 3/2, 8/12 and 4/9
Solution
On multiplying or dividing each term of a ratio by the same non zero number, we get a ratio equivalent to the given ratio
For, 8/12
Both numerator and denominator of given fraction is multiplied by same nonzero number i.e 4
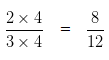
8/12 is an equivalent ratio of 2/3
3/2 is not an equivalent ratio of 2/3. As both 2 and 3 are not multiply by same non zero number
8/9 is not an equivalent ratio of 2/3. As both 2 and 3 are not multiply by same non zero number
4/9 is not an equivalent ratio of 2/3. As both 2 and 3 are not multiply by same non zero number
Ratio and Proportion Examples With Answers – Find the numbers when their ratio and sum are given
Example 3
Two numbers are in the ratio 3 : 5 and their sum is 160. Find the numbers?
Solution
Let the required number be 3a and 5a
Since the sum of these two numbers is given, we can say that
3a + 5a = 160
8a = 160
a = 160/8
a = 20
So, the first number is 3a = 3 x 20
= 60
Second number is 5a = 5 x 20
= 100
Hence, two numbers are 60 and 100
Ratio and Proportion Examples With Answers – Divide sum of money between two persons when ratio are given
Example 4
Divide ₹ 6000 among X and Y in the ratio 1 : 4
Solution
Total money = ₹ 6000
Given ratio = 1 : 4
Sum of ratio terms = ( 1 + 4 ) = 5
Give: 1/5 part of ₹ 6000 to X
Give: 4/5 part of ₹ 6000 to Y
that is,
X ‘s share = ₹ ( 6000 x 1/5) = ₹ 1200
Y ‘s share = ₹ ( 6000 x 4/5) = ₹ 4800
Ratio and Proportion Examples With Answers – Divide sum of money among 3 persons when ratio are given
Example 5
Divide ₹ 1800 among X , Y and Z in the ratio 3 : 4 : 1
Solution
Total money = ₹ 1800
Given ratio = 3 : 4 : 1
Sum of ratio terms = ( 3 + 4 + 1 ) = 8
X share = ₹ ( 1800 x 3/8) = ₹ 675
Y share = ₹ ( 1800 x 4/8) = ₹ 900
Z share = ₹ ( 1800 x 1/8) = ₹ 225
Ratio and Proportion Examples With Answers – Comparison of ratios
To Compare two Ratios, we should follow the following steps : –
- Write both the Ratios as Fractions
- Convert both the Fractions into Like Fraction:-
– Find the L.C.M of denominator of both the Fractions
– Make the denominator of each fraction equal to their L.C.M. - In case of Like fractions, the number whose numerator is greater is larger.
Example 6
Compare the ratios ( 2 : 5 ) and ( 3 : 4 )
Solution
We can write
( 2 : 5 ) = 2/5 and ( 3 : 4 ) = 3/4
Now, let us compare 2/5 and 3/4
LCM of 5 and 4 is 20
Making the denominator of each fraction equal to 20
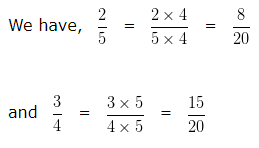
In case of Like fractions, the number whose numerator is greater is larger. Hence we can say 8/20 < 15/20
That is 2/5 < 3/4
Hence, ( 2 : 5 ) < ( 3 : 4 )
Ratio and Proportion Examples With Answers – Four Numbers in Proportion
Let a, b, c, d are four numbers said to be in proportion.
then, a : b = c : d or a : b :: c : d
here a and d are called the extreme terms or extremes.
b and c are called the middle terms or means.
When Four numbers are in proportion
then, Product of extremes = Product of means.
i.e, In proportion a : b :: c : d,
(a x d) = (b x c)
Ratio and Proportion Examples With Answers – Are the given number are in proportion
Example 7
Are 8 , 6 , 12 , 6 in proportion?
Solution
As we Know,
Product of extremes = Product of means
Here, Means are 6 and 12
Extremes are 8 and 6
Product of extremes = 8 x 6 = 48
Product of means = 6 x 12 = 72
Since, Product of extremes ≠ Product of means
Hence, 8 , 6 , 12 , 6 are not in Proportion
Ratio and Proportion Examples With Answers – Find the value of y when four numbers are in proportion
Example 8
If 6 : 9 : : y : 15, find the value of y?
Solution
We know that, Product of means = Product of extremes
In the given numbers, we can say that 9 , y are means and 6 , 15 are extremes
9 x y = 6 x 15
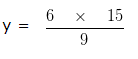
y = 10
Hence, y = 10